Problems

There are some incorrect weighing scales, a bag of cereal and a correct weight of 1 kg. How can you weigh on these scales 1 kg of cereals?

Can there exist two functions \(f\) and \(g\) that take only integer values such that for any integer \(x\) the following relations hold:

a) \(f (f (x)) = x\), \(g (g (x)) = x\), \(f (g (x)) > x\), \(g (f (x)) > x\)?

b) \(f (f (x)) < x\), \(g (g (x)) < x\), \(f (g (x)) > x\), \(g (f (x)) > x\)?

Michael thinks of a number no less than \(1\) and no greater than \(1000\). Victoria is only allowed to ask questions to which Michael can answer “yes” or “no” (Michael always tells the truth). Can Victoria figure out which number Michael thought of by asking \(10\) questions?

Can the equality \(K \times O \times T = U \times W \times E \times N \times H \times Y\) be true if the numbers from 1 to 9 are substituted for the letters? Different letters correspond to different numbers.

Deep in a forest there is a small town of talking animals. Elephant, Crocodile, Rabbit, Monkey, Bear, Heron and Fox are friends. They each have a landline telephone and each two telephones are connected by a wire. How many wires were required?

There are 6 locked suitcases and 6 keys to them. At the same time, it is not known to which suitcase each key fits. What is the smallest number of attempts you need to make in order to open all the suitcases for sure? And how many attempts will it take there are not 6 but 10 keys and suitcases?

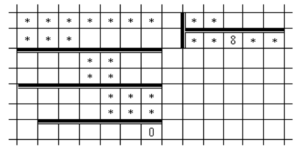
Decipher the following rebus (see the figure). Despite the fact that only two figures are known here, and all others are replaced by asterisks, the example can be restored.

The parliament of a certain country has two houses with an equal number of members. In order to make a decision on an important issue all the members voted and there were no abstentions. When the chairman announced that the decision had been taken with a 23-vote advantage, the opposition leader declared that the results had been rigged. How did he know it?

Among some number of mathematicians, every seventh is a philosopher, and among some number of philosophers every ninth is a mathematician. Who are there more of: philosophers or mathematicians?

Know-it-all came to visit the twin brothers Screw and Nut, knowing that one of them never speaks the truth, and asked one of them: “Are you Screw?”. “Yes,” he replied. When Know-it-all asked the second brother the same question, he received an equally clear answer and immediately determined who was who.

Who was called Screw?