Problems
At the end of the term, Billy wrote out his current singing marks in a row and put a multiplication sign between some of them. The product of the resulting numbers turned out to be equal to 2007. What is Billy’s term mark for singing? (The marks that he can get are between 2 and 5, where 5 is the highest mark).
Replace \(a, b\) and \(c\) with integers not equal to \(1\) in the equality \((ay^b)^c = - 64y^6\), so it would become an identity.
Sarah believes that two watermelons are heavier than three melons, Anna believes that three watermelons are heavier than four melons. It is known that one of the girls is right, and the other is mistaken. Is it true that 12 watermelons are heavier than 18 melons? (It is believed that all watermelons weigh the same and all melons weigh the same.)
A row of 4 coins lies on the table. Some of the coins are real and some of them are fake (the ones which weigh less than the real ones). It is known that any real coin lies to the left of any false coin. How can you determine whether each of the coins on the table is real or fake, by weighing once using a balance scale?
What is the largest number of counters that can be put on the cells of a chessboard so that on each horizontal, vertical and diagonal (not only on the main ones) there is an even number of counters?
Prove that for all \(x \in (0;\pi /2)\) for \(n > m\), where \(n, m\) are natural, we have the inequality \(2 | \sin^n x-\cos^n x | \leq 3 | \sin^m x-\cos^m x |\);
Is it possible to arrange natural numbers from 1 to \(2002^2\) in the cells of a \(2002\times2002\) table so that for each cell of this table one could choose a triplet of numbers, from a row or column, where one of the numbers is equal to the product of the other two?
All of the points with whole number co-ordinates in a plane are plotted in one of three colours; all three colours are present. Prove that there will always be possible to form a right-angle triangle from these points so that its vertices are of three different colours.
A regular hexagon with sides of length \(5\) is divided by straight lines, that are parallel to its sides, to form regular triangles with sides of length 1. We call the vertices of all such triangles nodes. It is known that more than half of the nodes are marked. Prove that there are five marked nodes lying on one circle.
Members of the State parliament formed factions in such a way that for any two factions \(A\) and \(B\) (not necessarily different)
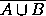
– also a faction (through
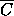
the set of all parliament members not included in \(C\) is denoted). Prove that for any two factions \(A\) and \(B\), \(A \cup % \includegraphics{https://problems-static.s3.amazonaws.com/production/problem_images/109909-3.png} B\) is also a faction.