Problems
Find \(x^3 +y^3\) if \(x+y=5\) and \(x+y+x^2 y +xy^2 =24\).
Along the path between Fiona’s and Jane’s house there is a row of flowers: 15 peonies and 15 tulips in a random order. Before visiting Fiona’s house, Jane started watering all of the plants from the beginning of the row. After the 10th tulip the water finished and 10 flowers were left unwatered. The next day, before visiting Jane’s house, Fiona started picking flowers for a bouquet starting from the end of the row. After picking the 6th tulip, she decided that the bouquet was big enough. How many flowers were left growing beside the path?
In a herd consisting of horses and camels (some with one hump and some with two) there are a total of 200 humps. How many animals are in the herd, if the number of horses is equal to the number of camels with two humps?
Of the four inequalities \(2x > 70\), \(x < 100\), \(4x > 25\) and \(x > 5\), two are true and two are false. Find the value of \(x\) if it is known that it is an integer.
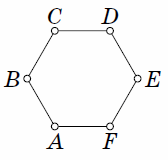
At the vertices of the hexagon \(ABCDEF\) (see Fig.) There were 6 identical balls: at \(A\) – one with mass 1 g, at \(B\) – 2 g, ..., at \(F\) – 6 g. Callum changed the places of two balls in opposite vertices. A set of weighing scales with 2 plates is available, which let you know which plate contains the balls of greater mass. How, in one weighing, can it be determined which balls were rearranged?
There are 40 weights of weights of 1 g, 2 g, ..., 40 grams. Of these, 10 weights of even weight were chosen and placed on the left hand side of the scales. Then we selected 10 weights of odd weight and put it on the right hand side of the scales. The scales were balanced. Prove that on one of the bowls of the scales there are two weights with a mass difference of 20 g.
Mark has 1000 identical cubes, each of which has one pair of opposite faces which are coloured white, another pair which are blue and a third pair that are red. He made a large \(10 \times 10 \times 10\) cube from them, joining cubes to one another which have the same coloured faces. Prove that the large cube has a face which is solidly one colour.
Compute the following: \[\frac{(2001\times 2021 +100)(1991\times 2031 +400)}{2011^4}.\]
After a circus came back from its country-wide tour, relatives of the animal tamer asked him questions about which animals travelled with the circus.
“Where there tigers?”
“Yes, in fact, there were seven times more tigers than non-tigers.”
“What about monkeys?”
“Yes, there were seven times less monkeys than non-monkeys.”
“Where there any lions?”
What is the answer he gave to this last question?
There are 100 boxes numbered from 1 to 100. In one box there is a prize and the presenter knows where the prize is. The spectator can send the presented a pack of notes with questions that require a “yes” or “no” answer. The presenter mixes the notes in a bag and, without reading out the questions aloud, honestly answers all of them. What is the smallest number of notes you need to send to know for sure where the prize is?