Problems

Is it possible to arrange natural numbers from 1 to ${2002}^2$ in the cells of a $2002\times 2002$ table so that for each cell of this table one could choose a triplet of numbers, from a row or column, where one of the numbers is equal to the product of the other two?

A number set $M$ contains $2003$ distinct positive numbers, such that for any three distinct elements $a,b,c$ in $M$, the number $a^2+bc$ is rational. Prove that we can choose a natural number $n$ such that for any $a$ in $M$ the number $a\sqrt{n}$ is rational.

A numeric set $M$ containing 2003 distinct numbers is such that for every two distinct elements $a,b$ in $M$, the number $a^2+b\sqrt{2}$ is rational. Prove that for any $a$ in $M$ the number $q\sqrt{2}$ is rational.

All of the points with whole number co-ordinates in a plane are plotted in one of three colours; all three colours are present. Prove that there will always be possible to form a right-angle triangle from these points so that its vertices are of three different colours.

Is there a bounded function $f:\mathbb{R}\to \mathbb{R}$ such that $f(1)>0$ and $f(x)$ satisfies the inequality $f^2(x+y)\ge f^2(x)+2f(xy)+f^2(y)$ for all $x,y\in \mathbb{R}$?

Ten pairwise distinct non-zero numbers are such that for each two of them either the sum of these numbers or their product is a rational number.

Prove that the squares of all numbers are rational.

A regular hexagon with sides of length $5$ is divided by straight lines, that are parallel to its sides, to form regular triangles with sides of length 1. We call the vertices of all such triangles nodes. It is known that more than half of the nodes are marked. Prove that there are five marked nodes lying on one circle.

The polynomial $P(x)$ of degree $n$ has $n$ distinct real roots.

What is the largest number of its coefficients that can be equal to zero?

Members of the State parliament formed factions in such a way that for any two factions $A$ and $B$ (not necessarily different)

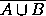
– also a faction (through

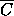
the set of all parliament members not included in $C$ is denoted). Prove that for any two factions $A$ and $B$, $A\cup B$ is also a faction.

We are given a table of size $n\times n$. $n-1$ of the cells in the table contain the number $1$. The remainder contain the number $0$. We are allowed to carry out the following operation on the table:

1. Pick a cell.

2. Subtract 1 from the number in that cell.

3. Add 1 to every other cell in the same row or column as the chosen cell.

Is it possible, using only this operation, to create a table in which all the cells contain the same number?