We solve problems

Problem #PRU-109946

Problems Algebra Algebraic equations and systems of equations Algebraic equations and systems of equations Calculus Real numbers Integer and fractional parts. Archimedean property Polynomials Quadratic polynomials Investigating the quadratic polynomial

14–15 3.0

Solve the equation \((x + 1)^3 = x^3\).

Problem #PRU-110047

Problems Algebra Rational and irrational numbers

13–15 3.0

We call a number \(x\) rational if it can be represented as \(x=\frac{p}{q}\) for coprime integers \(p\) and \(q\). Otherwise we call the number irrational.
Non-zero numbers \(a\) and \(b\) satisfy the equality \(a^2b^2 (a^2b^2 + 4) = 2(a^6 + b^6)\). Prove that at least one of them is irrational.

Problem #PRU-110061

Problems Methods Pigeonhole principle Pigeonhole principle (other)

13–16 4.0

Prove that in any set of 117 unique three-digit numbers it is possible to pick 4 non-overlapping subsets, so that the sum of the numbers in each subset is the same.

Problem #PRU-110072

Problems Combinatorics Dissections, partitions, covers and tilings Dissections with certain properties Geometry on grid paper Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

12–14 4.0

A target consists of a triangle divided by three families of parallel lines into 100 equilateral unit triangles. A sniper shoots at the target. He aims at a particular equilateral triangle and either hits it or hits one of the adjacent triangles that share a side with the one he was aiming for. He can see the results of his shots and can choose when to stop shooting. What is the largest number of triangles that the sniper can guarantee he can hit exactly 5 times?

Problem #PRU-110083

Problems Combinatorics Painting problems Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.) Algebra Word Problems Tables and tournaments Tables and tournaments (other)

12–14 3.0

Can the cells of a \(5 \times 5\) board be painted in 4 colours so that the cells located at the intersection of any two rows and any two columns are painted in at least three colours?

Problem #PRU-110103

Problems Algebra Number theory. Divisibility Division with remainders. Arithmetic of remainders Arithmetic of remainders Methods Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

Is it possible to arrange the numbers 1, 2, ..., 60 in a circle in such an order that the sum of every two numbers, between which lies one number, is divisible by 2, the sum of every two numbers between which lie two numbers, is divisible by 3, the sum of every two numbers between which lie six numbers, is divisible by 7?

Problem #PRU-110122

Problems Algebra Algebraic inequalities and systems of inequalities Algebraic inequalities (other) Calculus Functions of one variable. Continuity Monotonicity, boundedness

14–16 4.0

The functions \(f (x) - x\) and \(f (x^2) - x^6\) are defined for all positive \(x\) and increase. Prove that the function

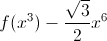
also increases for all positive \(x\).

Problem #PRU-110153

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

The sum of the positive numbers \(a, b, c\) is \(\pi / 2\). Prove that \(\cos a + \cos b + \cos c > \sin a + \sin b + \sin c\).

Problem #PRU-110157

Problems Geometry Plane geometry Plane transformations Similarity Homothetic transformations, rotations of homothetic transformations A homothetic transformation helps solve the problem Circles Connection between the arc length, the angle, and the chord Calculus Derivative Derivative and multiple roots Homothetic circles Tangent lines and tangent circles Tangent lines to circles Properties and criteria of a secant

14–16 5.0

The circles \(\sigma_1\) and \(\sigma_2\) intersect at points \(A\) and \(B\). At the point \(A\) to \(\sigma_1\) and \(\sigma_2\), respectively, the tangents \(l_1\) and \(l_2\) are drawn. The points \(T_1\) and \(T_2\) are chosen respectively on the circles \(\sigma_1\) and \(\sigma_2\) so that the angular measures of the arcs \(T_1A\) and \(AT_2\) are equal (the arc value of the circle is considered in the clockwise direction). The tangent \(t_1\) at the point \(T_1\) to the circle \(\sigma_1\) intersects \(l_2\) at the point \(M_1\). Similarly, the tangent \(t_2\) at the point \(T_2\) to the circle \(\sigma_2\) intersects \(l_1\) at the point \(M_2\). Prove that the midpoints of the segments \(M_1M_2\) are on the same line, independent of the positions of the points \(T_1, T_2\).

Problem #PRU-110166

Problems Set theory and logic Algorithm Theory Balance puzzles Methods Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

A set of weights has the following properties: It contains \(5\) weights, which are all different in weight. For any two weights, there are two other weights of the same total weight. What is the smallest number of weights that can be in this set?