We solve problems

Problems Discrete Mathematics Set theory and logic Mathematical logic Puzzles

Can I replace the letters with numbers in the puzzle \(RE \times CTS + 1 = CE \times MS\) so that the correct equality is obtained (different letters need to be replaced by different numbers, and the same letters must correspond to the same digits)?

Problem #PRU-115962

Problems Algebra Polynomials Algebraic identities for polynomials Factoring polynomials

12–14 2.0

Find \(x^3 +y^3\) if \(x+y=5\) and \(x+y+x^2 y +xy^2 =24\).

Problem #PRU-116009

Problems Algebra Graphs and locus of points on the Cartesian plane

13–15 2.0

On the \(xy\)-plane shown below is the graph of the function \(y=ax^2 +c\). At which points does the graph of the function \(y=cx+a\) intersect the \(x\) and \(y\) axes?

Problem #PRU-116021

Problems Algebra Algebraic inequalities and systems of inequalities Number inequalities. Number comparison

13–15 2.0

Find the largest natural number \(n\) which satisfies \(n^{200} <5^{300}\).

Problem #PRU-116023

Problems Number Theory Divisibility Divisibility rules Divisibility tests for 3 and 9 Methods Proof by contradiction

13–15 2.0

Does there exist a natural number which, when divided by the sum of its digits, gives a quotient and remainder both equal to the number 2011?

Problem #PRU-116055

Problems Algebra and arithmetic Arithmetics. Mental maths

11–12 2.0

Along the path between Fiona’s and Jane’s house there is a row of flowers: 15 peonies and 15 tulips in a random order. Before visiting Fiona’s house, Jane started watering all of the plants from the beginning of the row. After the 10th tulip the water finished and 10 flowers were left unwatered. The next day, before visiting Jane’s house, Fiona started picking flowers for a bouquet starting from the end of the row. After picking the 6th tulip, she decided that the bouquet was big enough. How many flowers were left growing beside the path?

Problem #PRU-116142

Problems Number Theory Equations in integer numbers

11–13 2.0

In a herd consisting of horses and camels (some with one hump and some with two) there are a total of 200 humps. How many animals are in the herd, if the number of horses is equal to the number of camels with two humps?

Problem #PRU-116145

Problems Algebra Algebraic inequalities and systems of inequalities Linear inequalites and systems of inequalities Discrete Mathematics Set theory and logic Logic and set theory

12–14 2.0

Of the four inequalities \(2x > 70\), \(x < 100\), \(4x > 25\) and \(x > 5\), two are true and two are false. Find the value of \(x\) if it is known that it is an integer.

Problem #PRU-116208

Problems Discrete Mathematics Algorithm Theory Balance puzzles

11–13 2.0

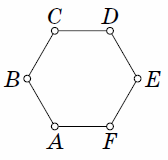
At the vertices of the hexagon \(ABCDEF\) (see Fig.) There were 6 identical balls: at \(A\) – one with mass 1 g, at \(B\) – 2 g, ..., at \(F\) – 6 g. Callum changed the places of two balls in opposite vertices. A set of weighing scales with 2 plates is available, which let you know which plate contains the balls of greater mass. How, in one weighing, can it be determined which balls were rearranged?

Problem #PRU-116239

Problems Discrete Mathematics Algorithm Theory Theory of algorithms (other)

10–12 2.0

There are 40 weights of weights of 1 g, 2 g, ..., 40 grams. Of these, 10 weights of even weight were chosen and placed on the left hand side of the scales. Then we selected 10 weights of odd weight and put it on the right hand side of the scales. The scales were balanced. Prove that on one of the bowls of the scales there are two weights with a mass difference of 20 g.