Problems

Age
Difficulty
 Clear filters
Found: 2621
Problem #PRU-5053
 13–16  4.0

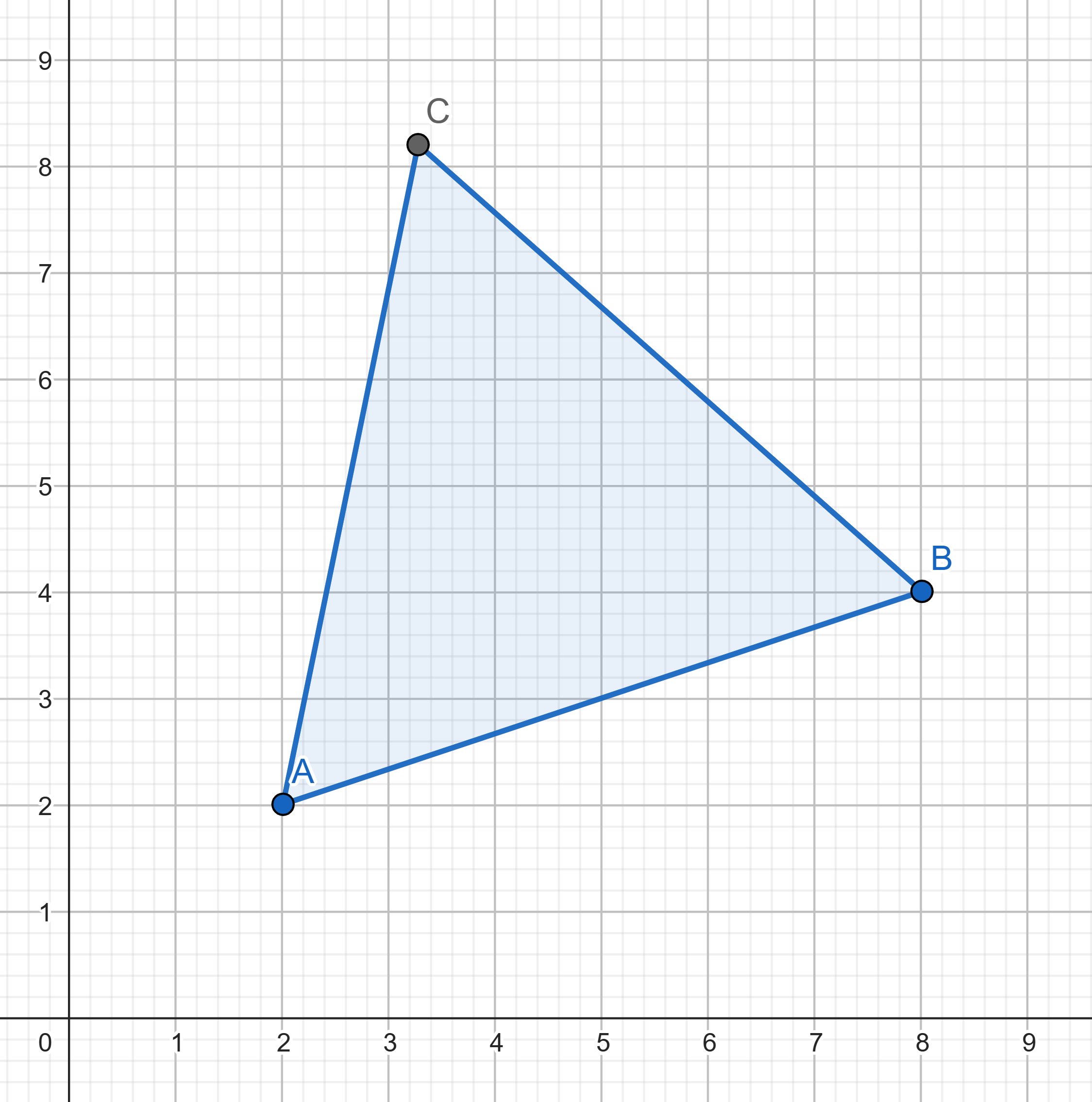
Can three points with integer coordinates be the vertices of an equilateral triangle?
image

Problem #PRU-5054
 10–15  1.0

Prove that there are infinitely many natural numbers \(\{1,2,3,4,...\}\).

Problem #PRU-5055
 10–15  4.0

Prove that there are infinitely many prime numbers \(\{2,3,5,7,11,13...\}\).

Problem #PRU-5056
 10–15  1.0

Is it possible to colour the cells of a \(3\times 3\) board red and yellow such that there are the same number of red cells and yellow cells?

Problem #PRU-5057
 11–14  2.0

Prove the divisibility rule for \(25\): a number is divisible by \(25\) if and only if the number made by the last two digits of the original number is divisible by \(25\);
Can you come up with a divisibility rule for \(125\)?

Problem #PRU-5058
 11–14  2.0

Which of the following numbers are divisible by \(11\) and which are not? \[121,\, 143,\, 286, 235, \, 473,\, 798, \, 693,\, 576, \,748\] Can you write down and prove a divisibility rule which helps to determine if a three digit number is divisible by \(11\)?

Problem #PRU-30345
 11–14  2.0

On a chessboard (an \(8 \times 8\) grid), we place eight identical rooks. A rook can move any number of squares in a straight line horizontally (along a row) or vertically (along a column). In chess, a piece can take another piece if it can move to the other piece’s square in a single move.

In how many ways can we arrange the eight rooks so that no rook can take any other?

Problem #PRU-60346
 11–14  2.0

How many five-digit numbers are there which are written the same from left to right and from right to left? For example the numbers \(54345\) and \(12321\) satisfy the condition, but the numbers \(23423\) and \(56789\) do not.

Problem #PRU-60399
 13–16  3.0

A set is a collection of elements where each element appears only once. The elements are not ordered, and there is no rule connecting them. Even a set with no elements (an empty set) counts as a set. The collections \(\{a,b,c,d\}\) and \(\{3,2,45,1,0,\pi\}\) are both examples of sets.

Let \(C\) be a set with \(n\) elements. How many different sets can be formed using the elements of \(C\)?

Problem #PRU-30336
 12–15  3.0

There are six letters in the alphabet of the Gloops. A word is any sequence of six letters that has at least two identical letters. How many words are there in the language of the Gloops?