Problems

Prove that the following facts are true for any graph:

a) The sum of degrees of all vertices is equal to twice the number of edges (and therefore it is even);

b) The number of vertices of odd degree is even.

There is a 12-litre barrel filled with beer, and two empty kegs of 5 and 8 litres. Try using these kegs to:

a) divide the beer into two parts of 3 and 9 litres;

b) divide the beer into two equal parts.

A traveller rents a room in an inn for a week and offers the innkeeper a chain of seven silver links as payment – one link per day, with the condition that they will be payed everyday. The innkeeper agrees, with the condition that the traveller can only cut one of the links. How did the traveller manage to pay the innkeeper?

During a chess tournament, some of the players played an odd number of games. Prove that the number of such players is even.

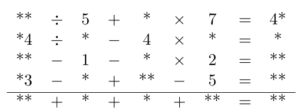
In the rebus in the diagram below, the arithmetic operations are carried out from left to right (even though the brackets are not written).

For example, in the first row "\(** \div 5 + * \times 7 = 4*\)" is the same as "\(((** \div 5) +*) \times 7 = 4*\)". Each number in the last row is the sum of the numbers in the column above it. The result of each \(n\)-th row is equal to the sum of the first four numbers in the \(n\)-th column. All of the numbers in this rebus are non-zero and do not begin with a zero, however they could end with a zero. That is, 10 is allowed but not 01 or 0. Solve the rebus.

There are scales without weights and 3 identical in appearance coins, one of which is fake: it is lighter than the real ones (the real coins are of the same weight). How many weightings are needed to determine the counterfeit coin? Solve the same problem in the cases where there are 4 coins and 9 coins.

We have scales without weights and 3 identical in appearance coins. One of the coins is fake, and it is not known whether it is lighter or heavier than the real coins (note that all real coins are of the same weight). How many weighings are needed to determine the counterfeit coin? Solve the same problem in the cases where there are 4 coins and 9 coins.

Decode this rebus: replace the asterisks with numbers such that the equalities in each row are true and such that each number in the bottom row is equal to the sum of the numbers in the column above it.

48 blacksmiths must shoe 60 horses. Each blacksmith spends 5 minutes on one horseshoe. What is the shortest time they should spend on the work? (Note that a horse can not stand on two legs.)

In Wonderland, an investigation was conducted into the case of a stolen soup. At the trial, the White Rabbit said that the soup was stolen by the Mad Hatter. The Cheshire Cat and the Mad Hatter also testified, but what they said, no one remembered, and the record was washed away by Alice’s tears. During the court session, it became clear that only one of the defendants had stolen the soup and that only he had given a truthful testimony. So, who stole the soup?