Problems
Recall that a line is tangent to a circle if they have only one point
of intersection, a circle is called inscribed in a polygon if it is
tangent to every side as a segment of that polygon.
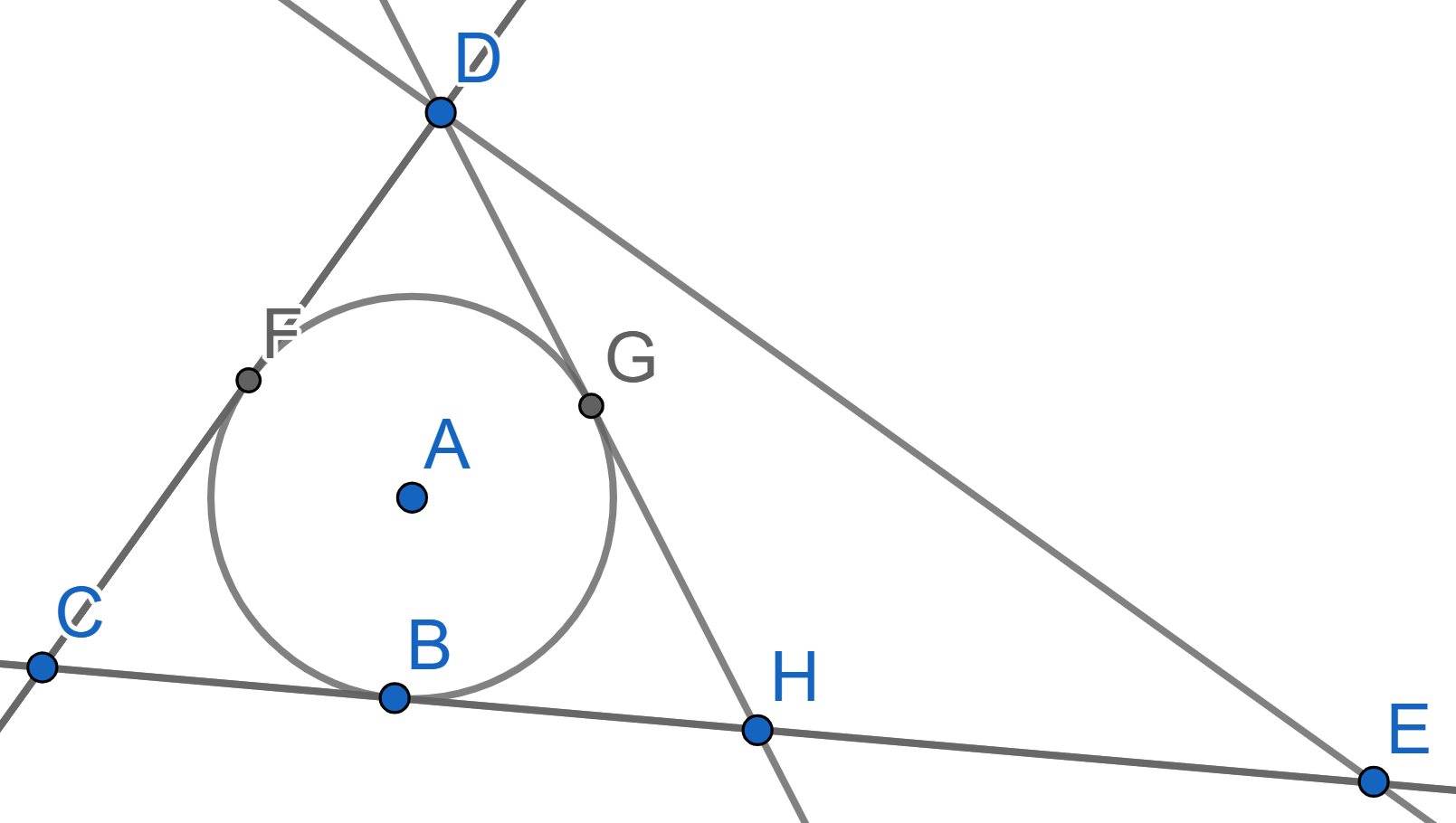
In the triangle \(CDE\) the angle \(\angle CDE = 90^{\circ}\) and the line
\(DH\) is the median. A circle with
center \(A\) is inscribed in the
triangle \(CDH\) and is tangent to the
segment \(DH\) in its middle, let’s
denote it as \(G\), so \(GH=DG\). Find the angles of the triangle
\(CDE\).
Recall that a line is tangent to a circle if they have only one point
of intersection, a circle is called inscribed in a polygon if it is
tangent to every side as a segment of that polygon.
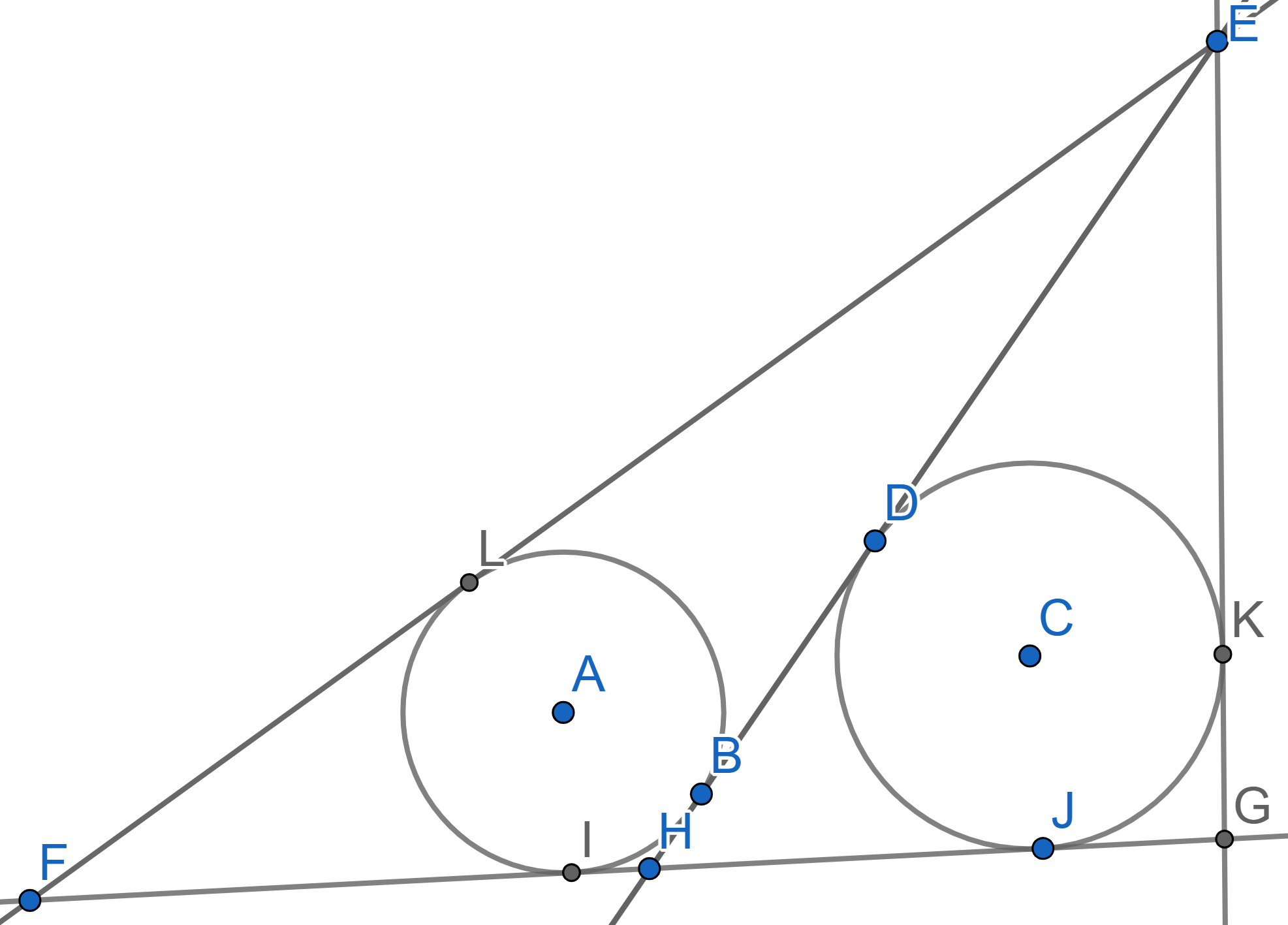
In the triangle \(EFG\) the line \(EH\) is the median. Two circles with
centres \(A\) and \(C\) are inscribed into triangles \(EFH\) and \(EGH\) respectively, they are tangent to the
median \(EH\) at the points \(B\) and \(D\). Find the length of \(BD\) if \(EF-EG=2\).
Is it possible to cover a \(6 \times 6\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.
Is it possible to cover a \((4n+2) \times (4n+2)\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.
Is it possible to cover a \(4n \times 4n\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.
There are \(100\) people standing in line, and one of them is Arthur. Everyone in the line is either a knight, who always tells the truth, or a liar who always lies. Everyone except Arthur said, "There are exactly two liars between Arthur and me." How many liars are there in this line, if it is known that Arthur is a knight?
Draw how Robinson Crusoe should use pegs, ropes, and sliding rings to tie his goat in order for the goat to graze grass in the shape of a square.
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a parallelogram.
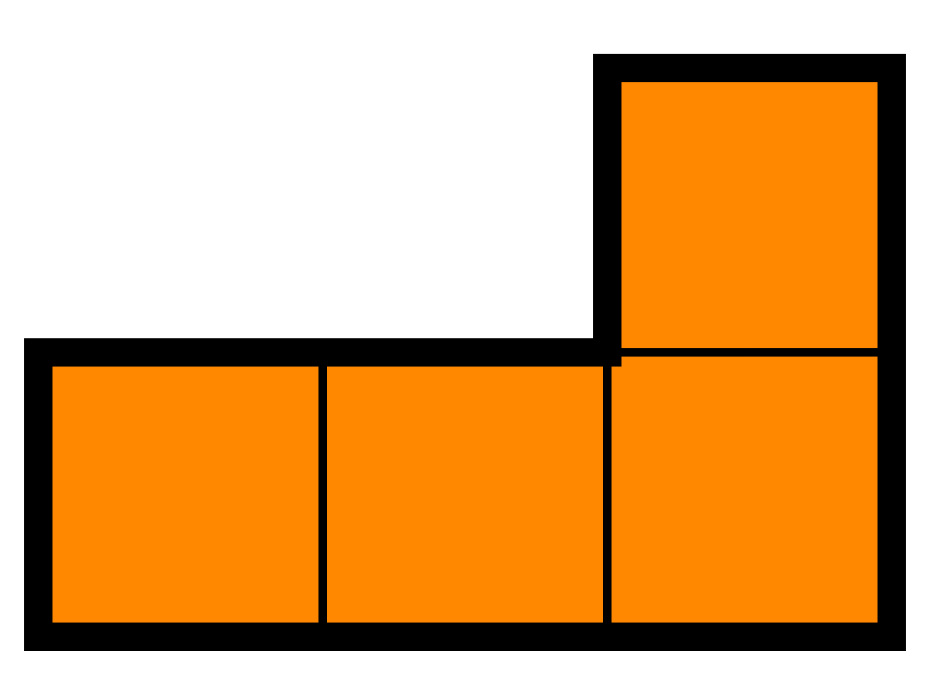
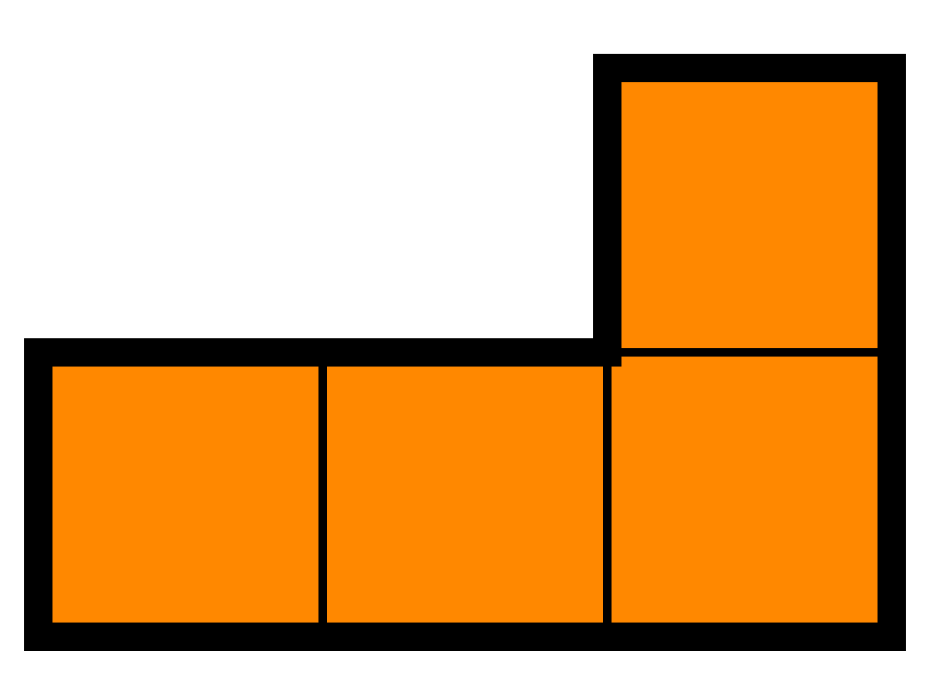
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in an area of the following shape:
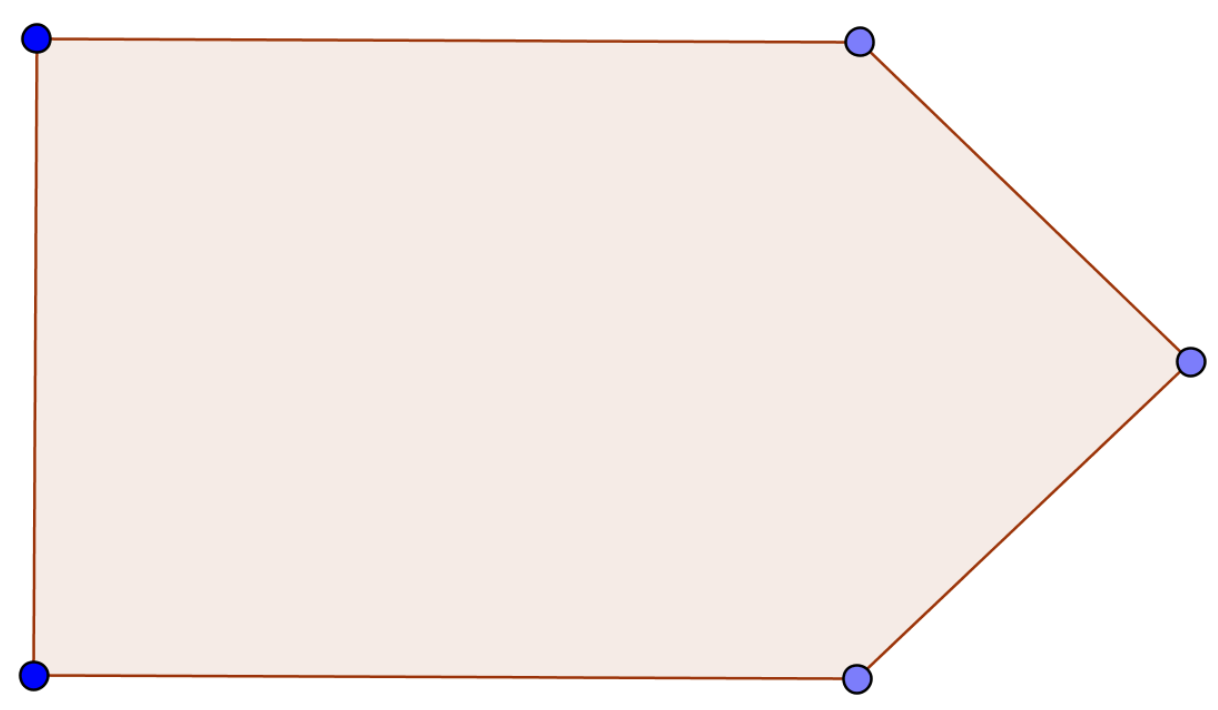
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.