Problems

A whole number of litres of water is distributed among three vessels. A legal move consists of choosing two vessels and pouring from one into the other exactly as many litres as the receiving vessel already contains. For example, if your vessels contain \((4,6,2)\) liters, then a legal move may be turning this into \((8,2,2)\). The vessels are large enough so that overflow never occurs.

Prove that after finitely many legal moves, one of the vessels can be made empty.

Roman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers are written as combinations of letters from the Latin alphabet, each letter with a fixed integer value:

For example the first \(12\) numbers in Roman Numerals are written as: \(I,\,II,\, III,\, IV,\, V,\, VI,\, VII,\, VIII,\, IX,\, X,\, XI,\, XII\), where the notations \(IV\) and \(IX\) can be read as "one less than five" and "one less than ten" correspondingly. A number containing two or more decimal digits is built by appending the Roman numeral equivalent for each digit, from highest to lowest, as in the following examples: the current year \(2024\) as \(MMXXIV\), number \(17\) as \(XVII\) and number \(42\) as \(XLII\) or \(XXXXII\). Let’s see how to multiply Roman numerals by multiplying \(17\) and \(42\).

Write down in Roman numerals the numbers \(14\) and \(61\) and multiply them as Roman numerals.

Detective Nero Wolf is investigating a crime. There are \(80\) people involved in the case. Among them, one is the criminal and another is the only witness to the crime (but the detective does not know who they are).

Each day, the detective may invite any group of these \(80\) people for questioning. If the group contains the witness but does not contain the criminal, then the witness will reveal who the criminal is. Otherwise, nothing happens.

Can the detective guarantee that he solves the case within \(12\) days?

A collection of weights is made from the weights \(1,2,4,8,\dots\) grams (that is, all powers of \(2\)). Some weights may appear several times. The weights are placed on the two pans of a balance scale and the scale is in balance. It is known that all the weights on the left pan are different.

Prove that the number of weights on the right pan is at least as large as the number of weights on the left pan.

Two lines \(CD\) and \(CB\) are tangent to a circle with the center \(A\) and radius \(R\), see the picture. The angle \(\angle BCD\) equals \(120^{\circ}\). Find the length of \(BD\) in terms of \(R\).

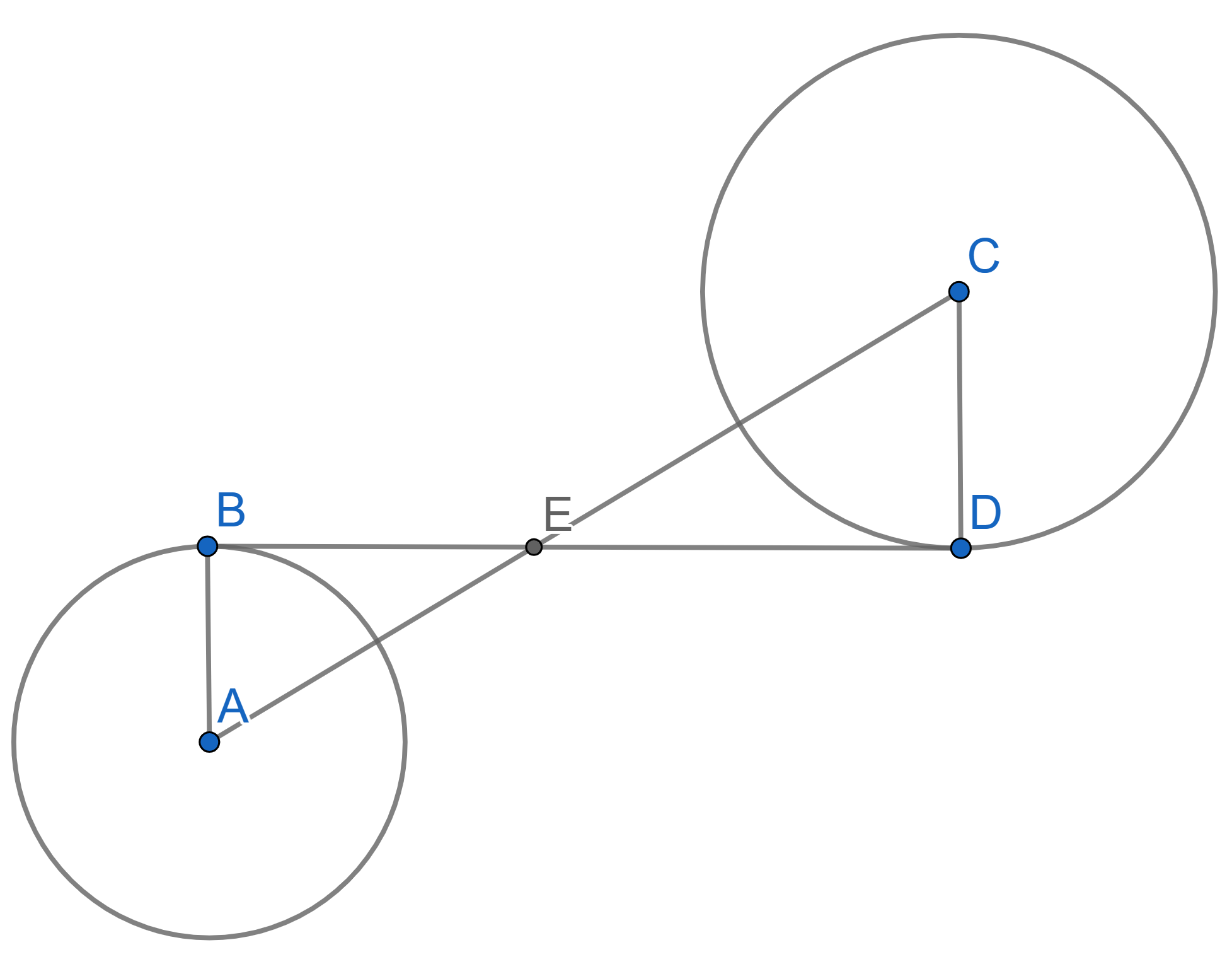
Given two circles, one has centre \(A\) and radius \(r\), another has centre \(C\) and radius \(R\). Both circles are tangent to a line at the points \(B\) and \(D\) respectively and the angles \(\angle CED = \angle AEB = 30^{\circ}\). Find the length of \(AC\) in terms of \(r\) and \(R\).

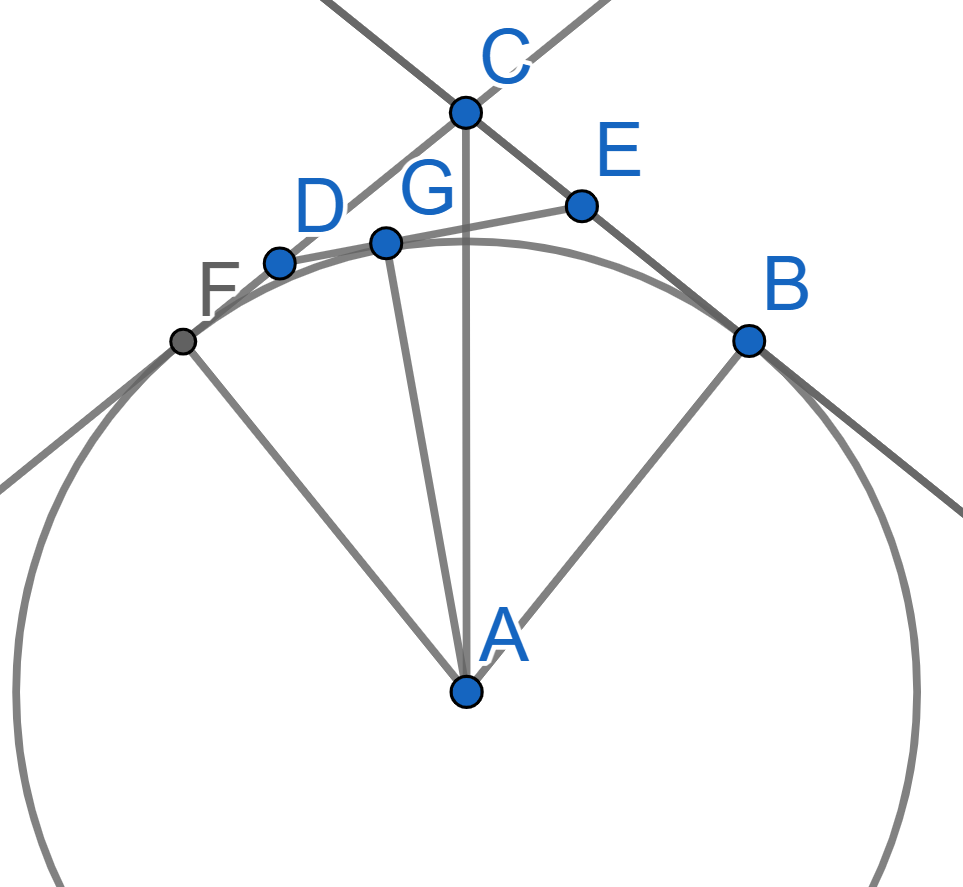
Consider a triangle \(CDE\). The lines \(CD\), \(DE\), and \(CE\) are tangent to a circle with centre \(A\) at the points \(F,G\), and \(B\) respectively. We also have that the angle \(\angle DCE = 120^{\circ}\). Prove that the length of the segment \(AC\) equals the perimeter of the triangle \(CDE\).

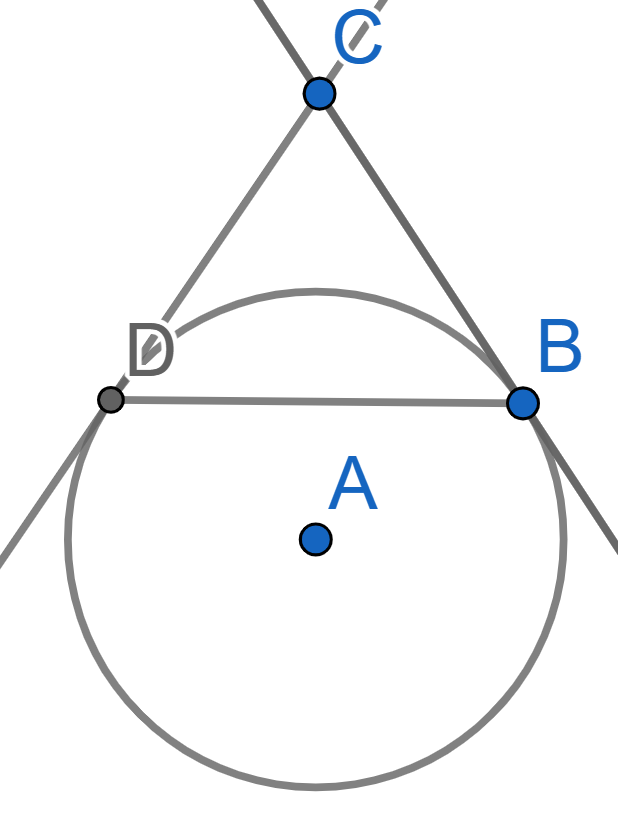
A circle with center \(A\) is tangent to the lines \(CB\) and \(CD\), see picture. Find the angles of the triangle \(BCD\) if \(BD=BC\).

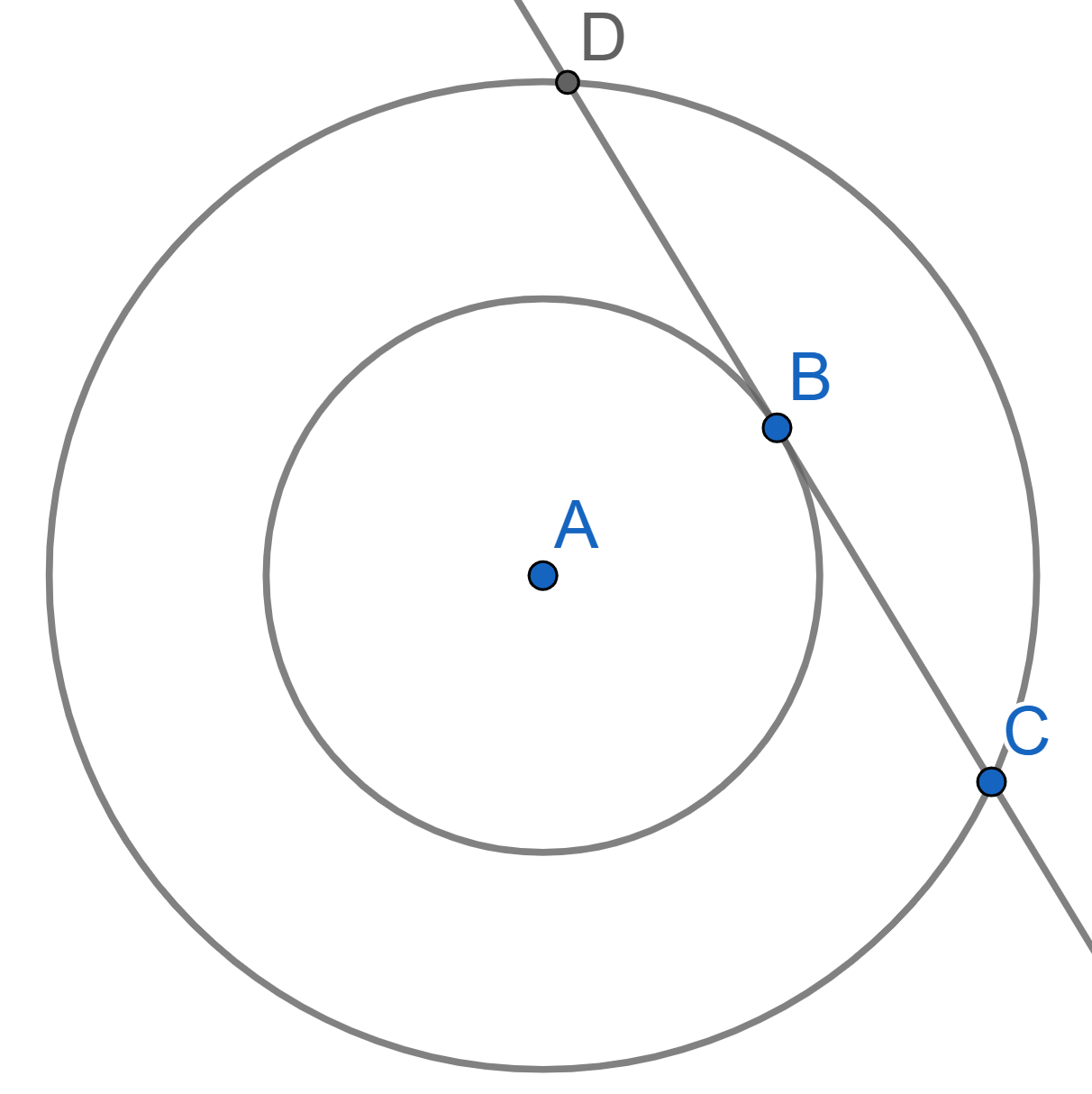
Take two circles with a common centre \(A\). A chord \(CD\) of the bigger circle is tangent to the smaller one at the point \(B\). Prove that \(B\) is the midpoint of \(CD\).