Problems
Find the mistake in the sequence of equalities: \(-1=(-1)^{\frac{2}{2}}=((-1)^2)^{\frac{1}{2}}=1^{\frac{1}{2}}=1\).
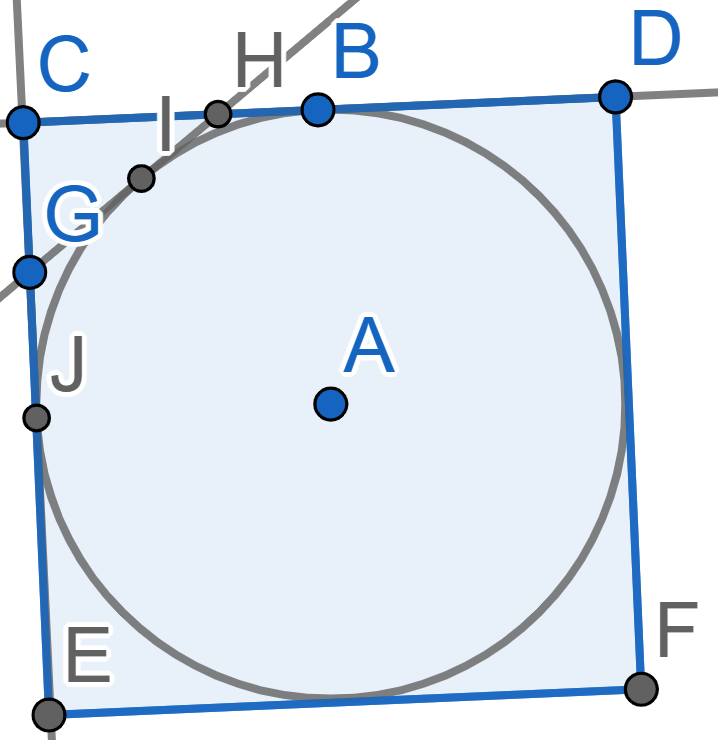
A circle with center \(A\) is inscribed into a square \(CDFE\). A line \(GH\) intersects the sides \(CD\) and \(CE\) of the square and is tangent to the circle at the point \(I\). Find the perimeter of the triangle \(CHG\) (the sum of lengths of all the sides) if the side of the square is \(10\)cm.
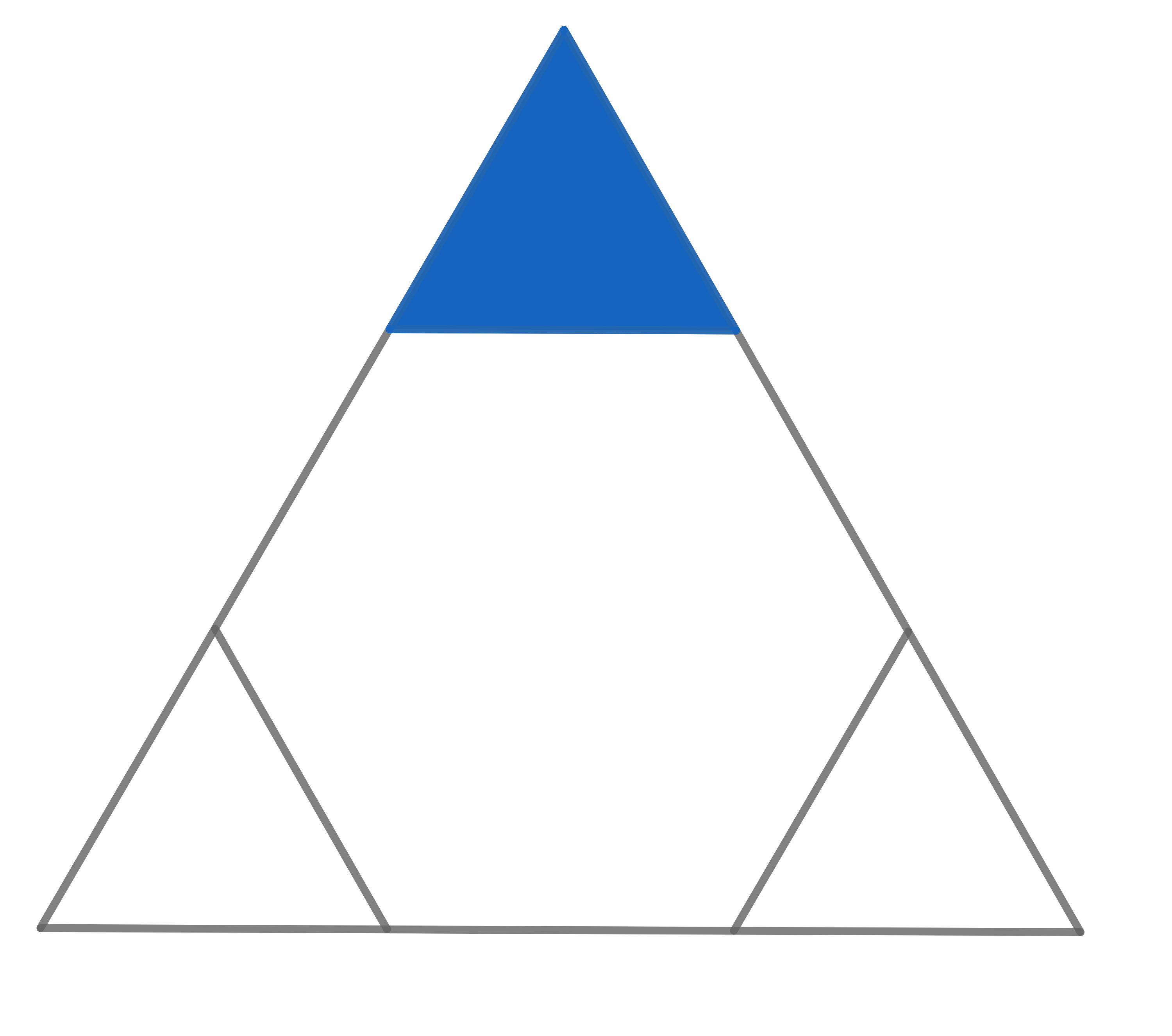
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.
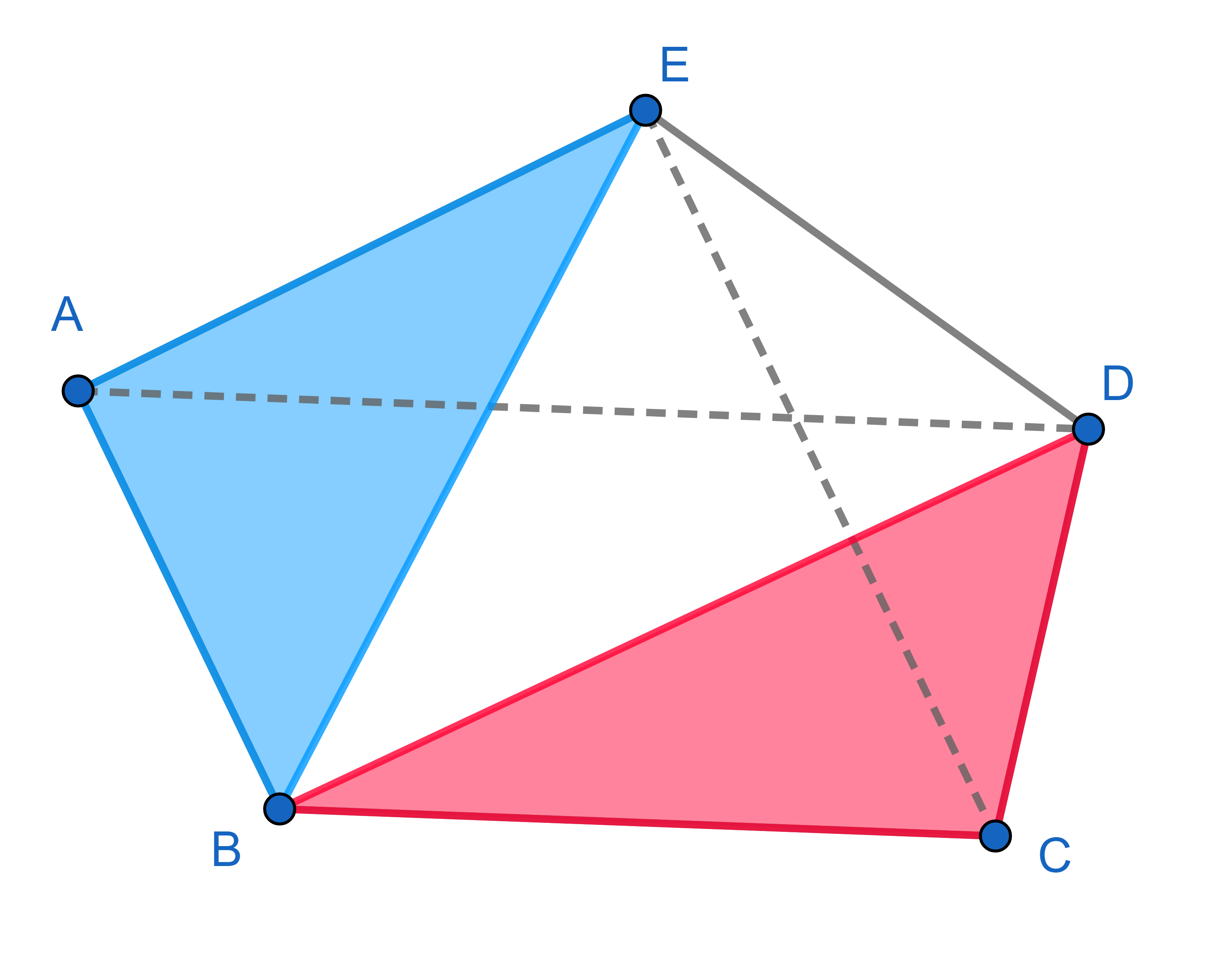
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.
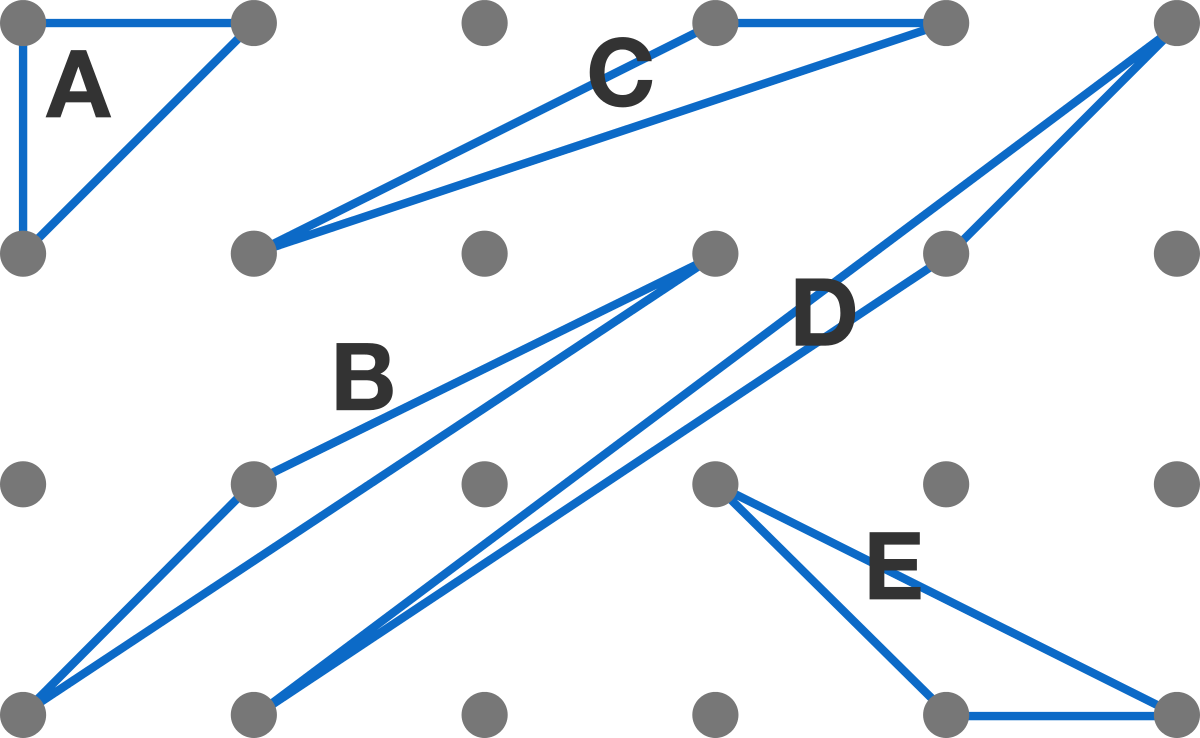
Which triangle has the largest area? The dots form a regular grid.
What is the ratio between the red and blue area? All shapes are semicircles and the red ones have equal radii.

In a parallelogram \(ABCD\), point \(E\) belongs to the side \(CD\) and point \(F\) belongs to the side \(BC\). Show that the total red area is the same as the total blue area:
The figure below is a regular pentagram. What is larger, the black area or the blue area?

This week we’re looking at Fibonacci numbers, and other sequences of numbers.
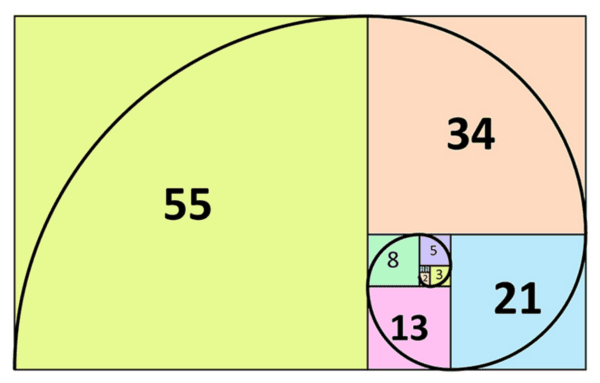
We say that the ‘zeroth’ Fibonacci number is \(0\) and the first Fibonacci number is \(1\). Then, from that point, every Fibonacci number is found by adding the two previous Fibonacci numbers. This means that the sequence begins \(0,1,1,2,3,5,8,13,21,34,55,89,144,...\)
The Fibonacci numbers hide lots of patterns which we’ll explore today. The spiral below is formed by taking squares whose side lengths are Fibonacci numbers, and drawing quarter circles in each square.
Prime numbers are like atoms that build every integer number. That is, a prime decomposition of a number is unique and then we can use it to find the number’s factors. Today we will explore this idea a bit more.
We will introduce a couple of new terms. First, a common divisor of two numbers is simply a number that both of these numbers can be divided by. Two numbers which have no common divisors (except from 1) are called relatively prime. We can establish if two numbers are relatively prime by looking at their prime factorizations - if they share no common primes, then they cannot share a common divisor!
Out of all the common divisors two numbers have, one must be the largest. This is an important number and is called the Greatest Common Divisor (GCD). You can find it by looking at the prime factorizations of the two numbers. For every prime number appearing in both factorizations, we take the smaller power. Then we multiply all our choices together. If we divide both numbers by their GCD, the resulting numbers will have no common divisors left and so will be relatively prime.
Similar to the notion of a common divisor is the one of common multiple. It is simply a number that is divisible by both numbers. Among the common multiples, one must be the smallest – this is called the Least Common Multiple (LCM). Again, the LCM can be found by looking at the prime factorizations of the two numbers. For every prime number appearing in any of the two factorizations, we take the larger power. Then we multiply all our choices together.