Problems
Tile a \(5\times6\) rectangle in an irreducible way by laying \(1\times2\) rectangles.
Does there exist an irreducible tiling with \(1\times2\) rectangles of a \(4\times 6\) rectangle?
Irreducibly tile a floor with \(1\times2\) tiles in a room that is a \(5\times8\) rectangle.
Tile the whole plane with the following shapes:
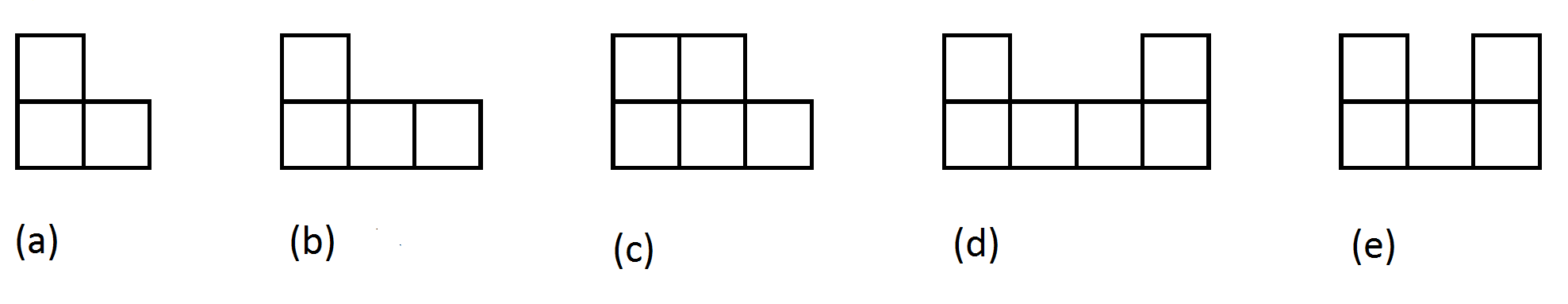
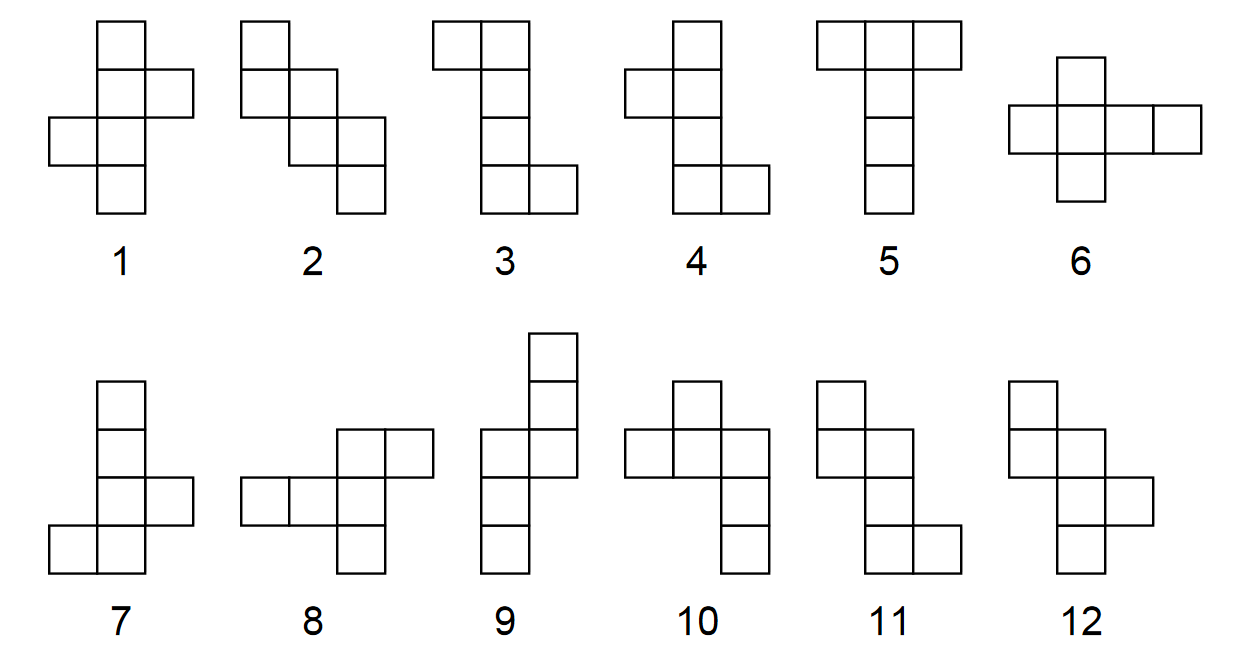
David Smith cut out 12 nets. He claimed that it was possible to make a cube out of each net. Roger Penrose looked at the patterns, and after some considerable thought decided that he was able to make cubes from all the nets except one. Can you figure out which net cannot make a cube?
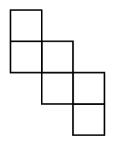
It is known that it is possible to cover the plane with any cube’s net. Show how you can cover the plane with this net:
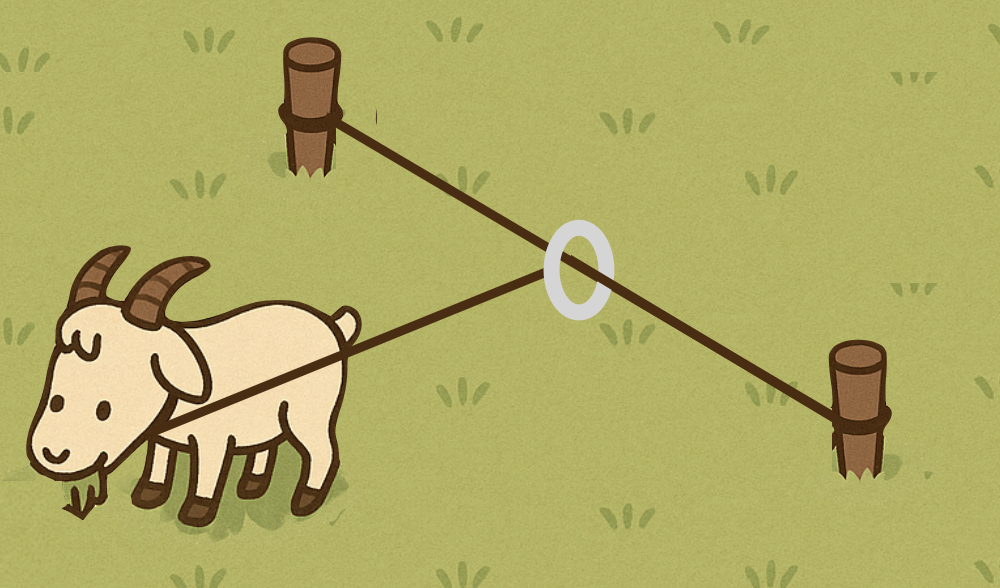
One day, Robinson Crusoe tied a rope tightly between two pegs, placed a sliding ring on it, and then tied the goat to the ring with another rope, as in the picture below. What shape did the goat graze this time?
On another day, Robinson Crusoe used two pegs again. This time, he tied one rope of length \(a\) to the first peg and another rope of length \(b\) to the second peg, both directly to the goat, so that it looked like in the picture below. What shape did the goat graze that day?

One day Robinson Crusoe went for a walk on a plateau, taking his goat with him on a rope of length one meter. He walked along a path in the shape of a rectangle measuring \(1 \,\text{km} \times 3 \,\text{km}\), following its perimeter. What was the shape of the area where the goat could graze while walking with Robinson?