Problems
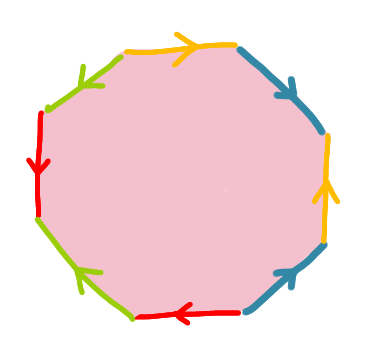
How would you describe the surface obtained by glueing the sides of the octagon as on the picture? Sides of the same colour are glued together in the same direction as shown.
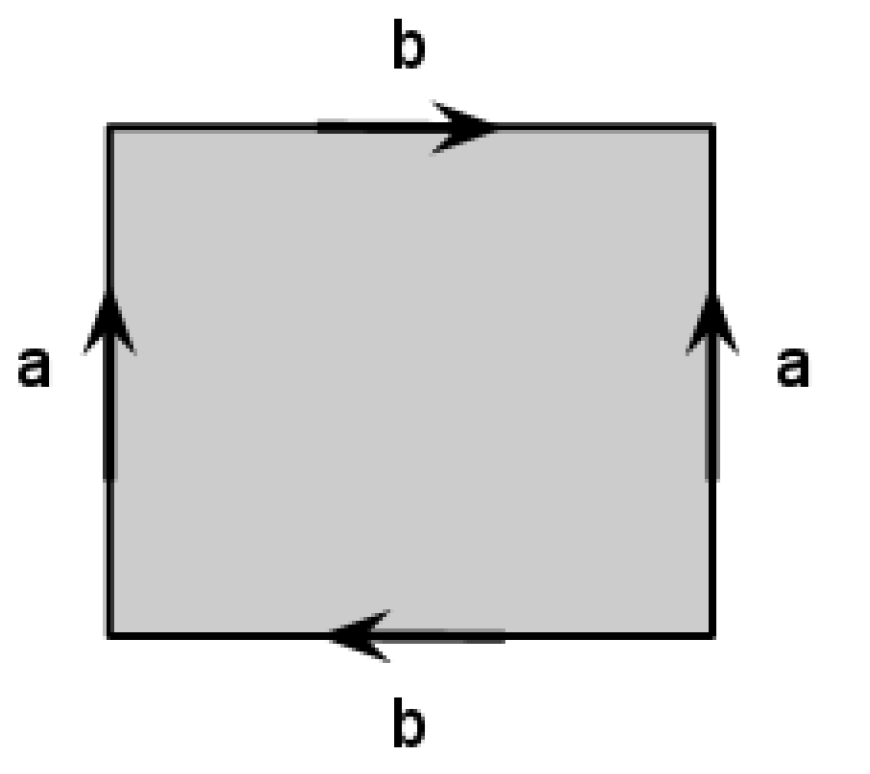
Describe the surface which we can get if we start with a rectangular sheet of paper, make a cylinder by glueing the opposite sides in the same direction and then glue the other opposite sides of the paper band in the opposite direction as on the picture.
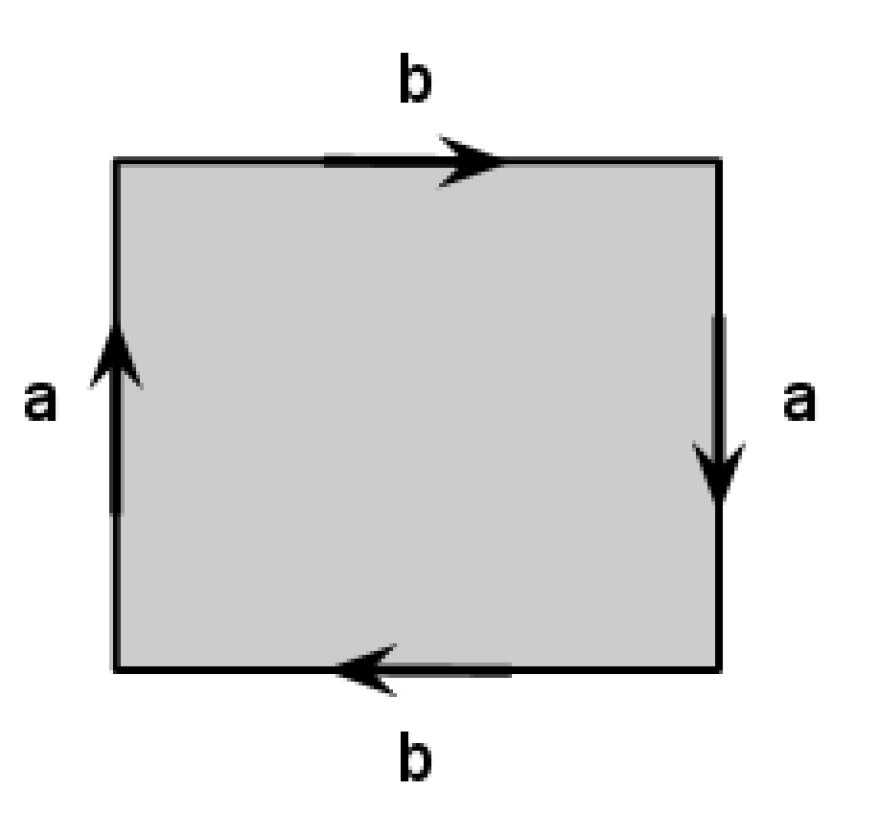
Describe the surface which we can get if we start with a rectangular sheet of paper, make a Moebius band by glueing the opposite sides in the opposite directions and then glue the other opposite sides of the paper band in the opposite direction as on the picture.
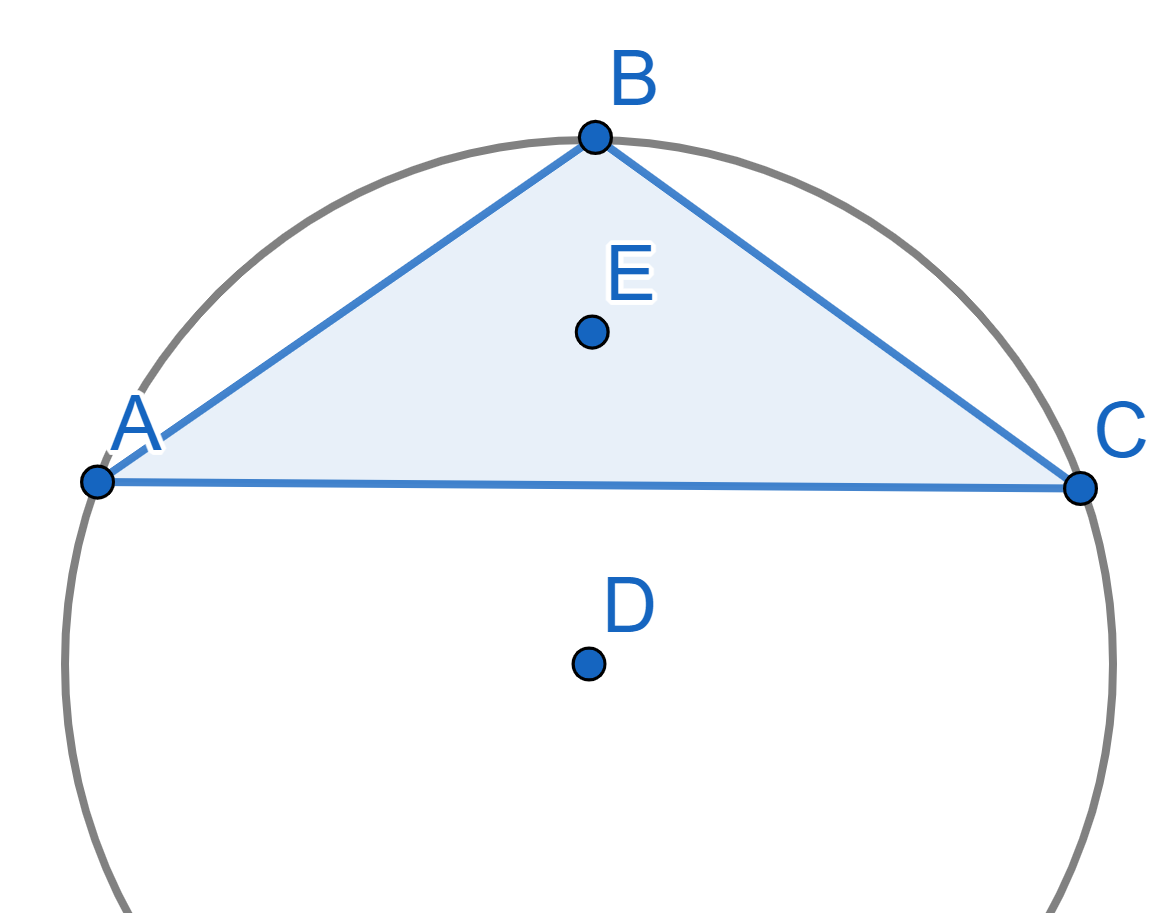
\(ABC\) is a triangle. The circumscribed circle is the circle that touches all three vertices of the triangle \(ABC\). It is also the smallest circle lying entirely outside the triangle. The center of the circumscribed circle is \(D\).
The inscribed circle is the circle which touches all three sides of the triangle \(ABC\). It is also the largest circle lying entirely inside the triangle. The center of the inscribed circle is \(E\).
The points \(D\) and \(E\) are symmetric with respect to the segment \(AC\). Find the angles of the triangle \(ABC\).
Scrooge McDuck has \(100\) golden coins on his office table. He wants to distribute them into \(10\) piles so that no two piles contain the same amount of coins. Moreover, no matter how you divide any of the piles into two smaller piles, among the resulting \(11\) piles there will be two with the same amount of coins. Find an example of how he could do that.
A parliament has 650 members. In this parliament there is only one house and every member has at most three enemies. We wish to split this parliament into two separate houses in such a way that each member will have at most one enemy in the same house as them. We assume that hard feelings among members of parliament are mutual, namely if \(A\) recognises \(B\) as their enemy, then \(B\) also recognises \(A\) as their enemy.
Is this splitting possible?
Today we will draw lots of pictures.
The subject is Topology. It is often called “rubber-sheet geometry" because while it is the study of shapes, topologists typically do not pay too much attention to rigid notions like angle and lengths. We have much more flexibility in topology. Some common words describing the operations here might include “gluing", “stretching", “twisting" and “inflating".
Although we will not define continuity, it is a more or less intuitive idea. Topological operations should be continuous. If you have a line segment, no amount of stretching, twisting or bending can make it into two disconnected segments.
We can define the absolute value \(|x|\) of any real number \(x\) as follows. \(|x|=x\) if \(x\ge0\) and \(|x|=-x\) if \(x<0\). What are \(|3|\), \(|-4.3|\) and \(|0|\)?
Prove that \(|x|\ge0\).
Prove that \(|x|\ge x\). It may be helpful to compare each of \(|3|\), \(|-4.3|\) and \(|0|\) with \(3\), \(-4.3\) and \(0\) respectively.
Let \(A=\{1,2,3\}\) and \(B=\{2,4\}\) be two sets containing natural numbers. Find the sets: \(A\cup B\), \(A\cap B\), \(A-B\), \(B-A\).