Problems

A simple polygon is a polygon that does not intersect itself and has no holes. Suppose we have a simple polygon \(S\) whose vertices consists of only integer coordinates.

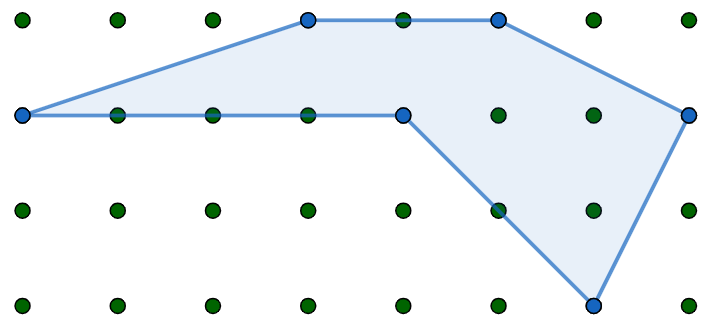
The area turns out to be remarkably easy to calculate. Count up the number of points with integer coordinate inside the polygon and on the boundary; call them \(i\) and \(b\) respectively. The area is then \[A(S) = i+\frac{b}{2}-1.\]

In the picture above, \(i=3\) and \(b=11\), so \(A(S) = \frac{15}{2}\). Prove that this formula for the area \(A(S)\) is correct.

Let \(\phi(n)\) be Euler’s function. Namely \(\phi(n)\) counts how many integers from \(1\) to \(n\) inclusive are coprime with \(n\). For two natural numbers \(m\), \(n\) such that \(\gcd(m,n)=1\), prove that \(\phi(mn) = \phi(m)\phi(n)\).

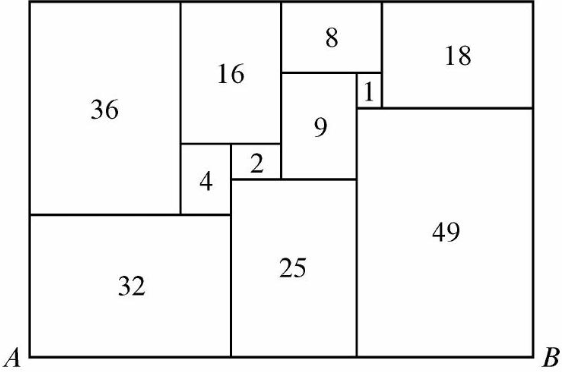
All of the rectangles in the figure below, which is drawn to scale, are similar to the big rectangle (that is, their sides are in the same ratio). Each number represents the area of the rectangle. What is the length \(AB\)?

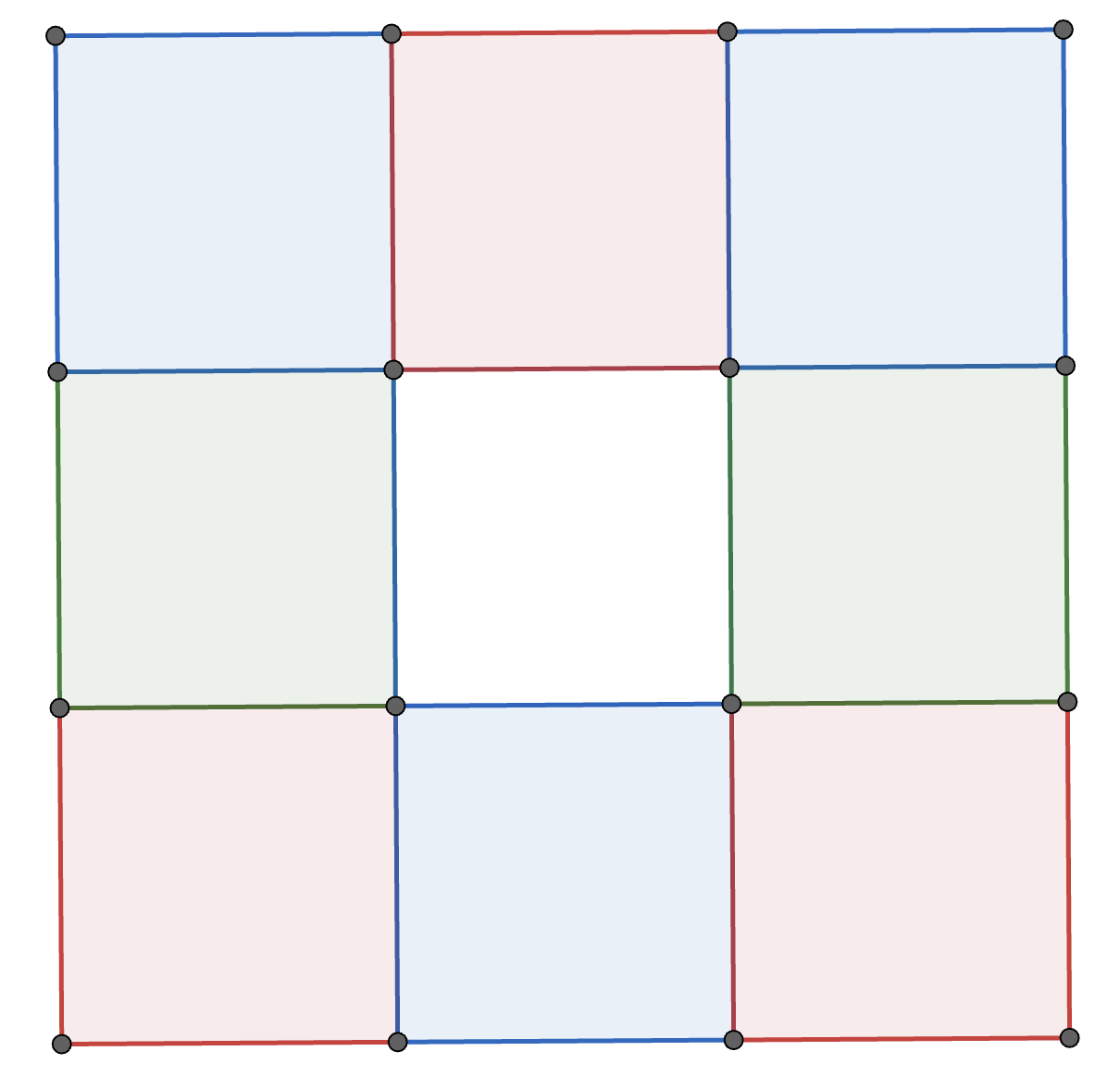
Each square in a \(3\times3\) grid of squares is coloured red, white, blue, or green so that every \(2\times2\) square contains one square of each color. One such colouring is shown below. How many different colourings are possible?

For any positive integer \(k\), the factorial \(k!\) is defined as a product of all integers between 1 and \(k\) inclusive: \(k! = k \times (k-1) \times ... \times 1\). What’s the remainder when \(2025!+2024!+2023!+...+3!+2!+1!\) is divided by \(8\)?

There are two imposters and seven crewmates on the rocket ‘Plus’. How many ways are there for the nine people to split into three groups of three, such that each group has at least two crewmates? The two imposters and seven crewmates are all distinguishable from each other, but we’re not concerned with the order of the three groups.

For example: \(\{I_1,C_1,C_2\}\), \(\{I_2,C_3,C_4\}\) and \(\{C_5,C_6,C_7\}\) is the same as \(\{C_3,C_4,I_2\}\), \(\{C_5,C_6,C_7\}\) and \(\{I_1,C_2,C_1\}\) but different from \(\{I_2,C_1,C_2\}\), \(\{I_1,C_3,C_4\}\) and \(\{C_5,C_6,C_7\}\).

Let \(n\) be a natural number, and let \(d(n)\) be the number of factors of \(n\). For example, the factors of \(6\) are \(1,2,3,6\), so \(d(6)=4\). Find all \(n\) such that \(d(n)+d(n+1)=5\).

Draw the plane tiling with regular hexagons.

Let \(\sigma(n)\) be the sum of the divisors of \(n\). For example, \(\sigma(12)=1+2+3+4+6+12=28\). We use \(\gamma\) to denote the Euler-Mascheroni constant - one way to define this is as \(\gamma:=\lim_{n\to\infty}(\sum_{k=1}^n\frac{1}{n}-\log n)\).

Prove that \(\sigma(n)<e^{\gamma}n\log\log n\) for all integers \(n>5040\).

Let \(a\) and \(b\) be two different \(9\)-digit numbers. It is known that each one of them contains all of the digits \(1,2,...9\). Find the maximal value of \(\gcd(a,b)\).