Problems
Just like atoms are the building blocks of molecules, prime numbers are the building blocks of integers, or whole numbers. What do we mean by this?
Well, every molecule is composed of atoms, and each atom is an atom of a particular element, like carbon or nitrogen. Similarly, every positive integer (except \(1\)) can be broken down into prime numbers. We can say this formally as follows:
The Fundamental Theorem of Arithmetic says that any natural number greater than \(1\) can be uniquely expressed as a product of prime numbers in non-decreasing order. For example: \[630=2\times3\times3\times5\times7=2\times3^2\times5\times7.\]
Recall that a number is composite if it is a product of two smaller, natural numbers. For example, \(6 = 2\times3\). Otherwise, and if the number is not equal to \(1\), it is called prime. The number \(1\) is neither prime nor composite.
Modulo operation: We look at division. For example \(41=2\times15+11\) is the division of \(41\) (the dividend) by \(15\) (the divisor) with remainder
\(11\), and \(5=0\times7+5\) is the division of \(5\) by \(7\) with the remainder \(5\). More generally, when we divide \(a\) by \(b\), we’re looking for non-negative
integers \(c\) and \(d\) (\(d<b\)) such that \(a=c\times b+d\).
In the case of \(45\) divided by \(15\), we get \(3\) with remainder \(0\) - in which case we say “\(15\) divides \(45\)", or “\(45\) is divisible by \(15\)". We can write this as \(15|45\).
We can deduce from the Fundamental Theorem of Arithmetic that if a product of two natural numbers is divisible by a prime number, then one of these numbers is divisible by this prime number. For example, \(7|7007=13\times539\) tells us that \(7\) divides \(13\) or \(539\). Clearly \(7\nmid13\), so we know \(7|539\).
It is often the case in geometric situations that figures look very
similar, but not quite equal. Two polygons on the plane are called
similar if and only if ALL their corresponding angles
are equal AND the ratio between ALL
the corresponding sides is the same.
The relation between the corresponding sides, in our case it’s \(\frac{|AB|}{|IH|}\), is called the
similarity coefficient between the figures. It is common practice to
write vertices of similar figures in the order that respects the
similarity.
We will find some criteria for determining similarity and apply them to solve problems. The statements of some examples and problems may be helpful for problems coming after them!
Let \(\triangle ABC\) and \(\triangle DEF\) be triangles such that the following angles are equal: \(\angle ABC = \angle DEF\) and \(\angle ACB = \angle DFE\). Prove that \(\triangle ABC\) and \(\triangle DEF\) are similar triangles.
The medians \(AD\) and \(BE\) of the triangle \(\triangle ABC\) intersect at the point \(F\). Prove that \(\triangle AFB\) and \(\triangle DFE\) are similar. What is their similarity coefficient?
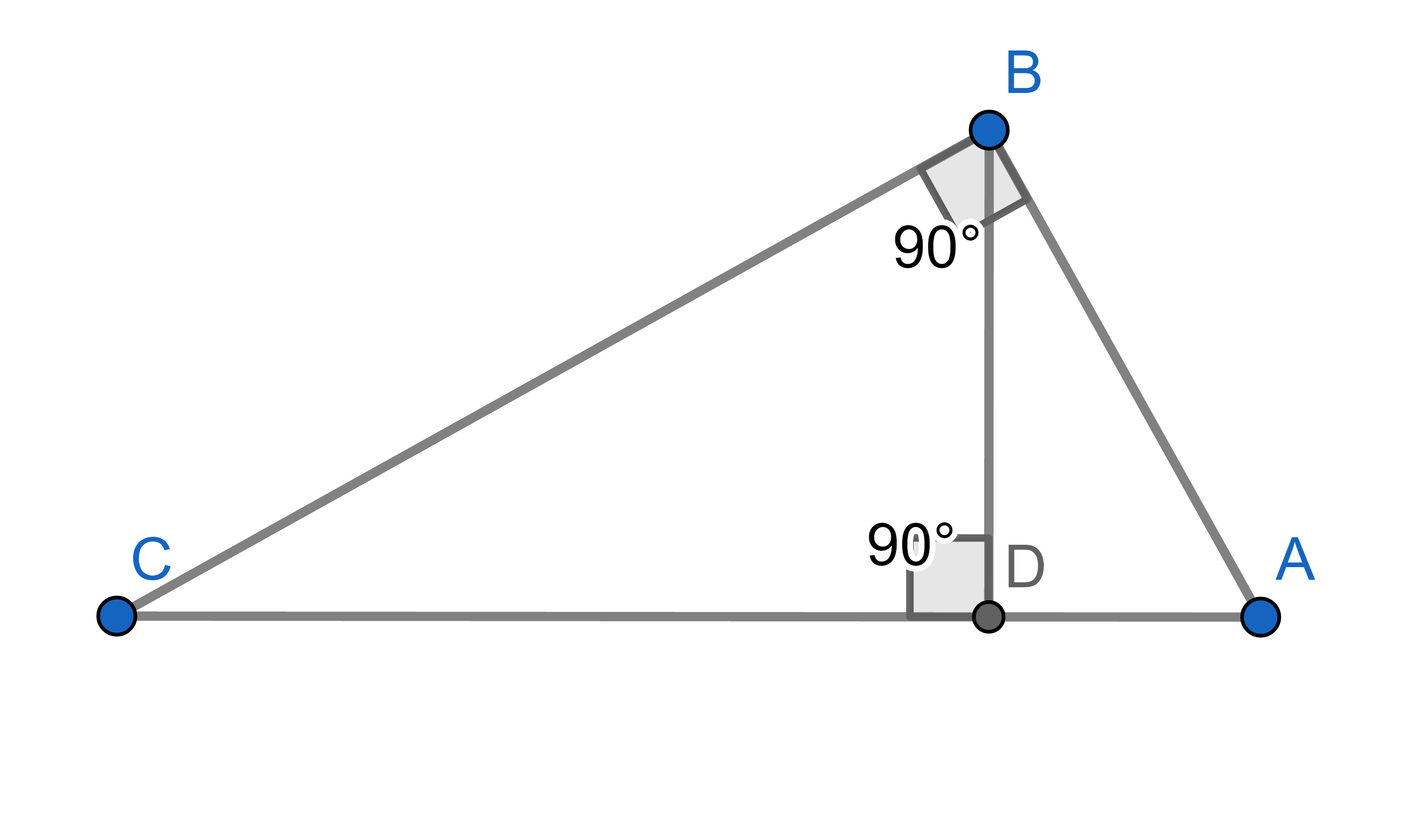
In a triangle \(\triangle ABC\), the angle \(\angle B = 90^{\circ}\) . The altitude from point \(B\) intersects \(AC\) at \(D\). We know the lengths \(|AD|=9\) and \(|CD|=25\). What is the length \(|BD|\)?
Let \(\triangle ABC\) and \(\triangle DEF\) be two triangles such that \(\angle ACB = \angle DFE\) and \(\frac{|DF|}{|AC|} = \frac{|EF|}{|BC|}\). Prove that \(\triangle ABC\) and \(\triangle DEF\) are similar.
Let \(AA_1\) and \(BB_1\) be the medians of the triangle \(\triangle ABC\). Prove that \(\triangle A_1B_1C\) and \(\triangle BAC\) are similar. What is the similarity coefficient?
Let \(AD\) and \(BE\) be the heights of the triangle \(\triangle ABC\), which intersect at the point \(F\). Prove that \(\triangle AFE\) and \(\triangle BFD\) are similar.
Let \(AD\) and \(BE\) be the heights of the triangle \(\triangle ABC\). Prove that \(\triangle DEC\) and \(\triangle ABC\) are similar.
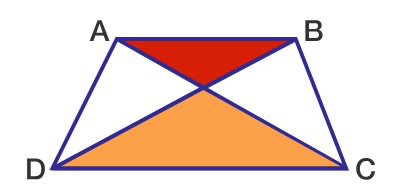
The area of the red triangle is \(25\) and the area of the orange triangle is \(49\). What is the area of the trapezium \(ABCD\)?