Problems

How many paths are there from the $1$ at the top (in the ‘zeroth’ row) to the first $70$, which appears in the middle of the eighth row?

These paths go down at each step to a number either to the left or to the right. An example is (the first $1$), $1$, $2$, $3$, $6$, $10$, $15$, $35$ and then $70$ to finish.

What’s the sum of the squares of the numbers in the $n^{\text{th}}$ row?

Let $p$ be a prime number. What do you notice about the numbers other than $1$ in the $p^{\text{th}}$ row? Can you prove it?

The picture below shows the ‘hockey-stick’ identity in Pascal’s triangle.

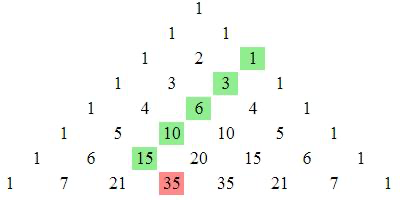
It says that if you start one of the diagonals formed of $1$s at the edge, then follow the numbers diagonally in one direction (e.g. left in the picture) and then change direction on your final turn (right in the picture), then the sum of the all but the last number is equal to the last number.

Prove this is true. Written algebraically, $$(\genfrac{}{}{0ex}{}{r}{r})+(\genfrac{}{}{0ex}{}{r+1}{r})+...+(\genfrac{}{}{0ex}{}{n-1}{r})+(\genfrac{}{}{0ex}{}{n}{r})=(\genfrac{}{}{0ex}{}{n+1}{r+1}),$$ where $0\le r\le n$.

In the $n^{\text{th}}$ row of Pascal’s triangle, leave the left $1$ untouched, multiply the next number along (which is $(\genfrac{}{}{0ex}{}{n}{1})=n$) by $2$, multiply the next number along (which is $(\genfrac{}{}{0ex}{}{n}{2})=\frac{n(n-1}{2}$) by $4$, and so on, until you multiply the right-hand $1$ by $2^n$. That is, multiply the $k^{\text{th}}$ number from the left by $2^k$.

Now what’s the sum of the numbers in the $n^{\text{th}}$ row?

Let $s_n$ be the product of the numbers in the $n^{\text{th}}$ row. (e.g. $s_3=1\cdot 3\cdot 3\cdot 1=9$) What’s the limit $$\underset{n\to \mathrm{\infty }}{lim}\frac{s_{n-1}{s}_{n+1}}{s_n^2}?$$

Other than $1$, does any number appear more than eight times in Pascal’s triangle?

Some randomly chosen people are in a room. A mathematician walks in and says that the probability that there exist at least two people with the same birthday is just over $50\mathrm{\%}$. How many people are in the room?

Today we’ll look at various problems involving probability. [do we need more of an introduction?]

Imagine there’s a disease called ‘mathematitis’ which $1\mathrm{\%}$ of people have. Doctors create a new test to discover whether people have mathematitis. The doctors fine-tune the test until it’s $99\mathrm{\%}$ accurate - that is, if a person $A$ has it, then $99\mathrm{\%}$ of the time the test will say that $A$ has it, and $1\mathrm{\%}$ of the time the test will say that $A$ doesn’t have mathematitis.

Additionally, for person $B$ who doesn’t have the disease, $99\mathrm{\%}$ of the time the test will correctly identify that $B$ doesn’t have it - and the other $1\mathrm{\%}$ of the time, the test will say that $B$ does have mathematitis.

Suppose you don’t know whether you have mathematitis, so you go to the doctors to take this test, and the test says you’ve got it! What’s the probability that you do actually have the disease?