Problems

Let \(a, b, c\) be numbers such that \(a^2 + b^2 + c^2 = 1\). Show that \[-\frac12 \leq ab + bc + ac \leq 1.\]

An ordered triple of numbers is given. It is permitted to perform the following operation on the triple: to change two of them, say \(a\) and \(b\), to \(\frac{a+b}{\sqrt{2}}\) and \(\frac{a-b}{\sqrt{2}}\). Is it possible to obtain the triple \((1,\sqrt{2},1+\sqrt{2})\) from the triple \((2,\sqrt{2},\frac{1}{\sqrt{2}})\) using this operation?

(USAMO 1997) Let \(p_1, p_2, p_3,\dots\) be the prime numbers listed in increasing order, and let \(0 < x_0 < 1\) be a real number between 0 and 1. For each positive integer \(k\), define \[x_k = \begin{cases} 0 & \text{ if } x_{k-1} = 0 \\ \left\{\frac{p_k}{x_{k-1}} \right\} & \text{ if } x_{k-1} \neq 0 \end{cases}\] where \(\{x\}\) denotes the fractional part of \(x\). For example, \(\{2.53\} = 0.53\) and \(\{3.1415926...\} = 0.1415926...\). Find, with proof, all \(x_0\) satisfying \(0 <x_0 <1\) for which the sequence \(x_0, x_1, x_2,\dots\) eventually becomes 0.

Take the number \(2026^{2026}\). We remove the leading digit and add it to the remaining number. This action is repeated until there are exactly \(10\) digits left. Show that there must be two digits that are the same in the end.

Every even number is not prime. The number \(9\) is not an even number, therefore it is not not prime, i.e: the number \(9\) is prime.

In a school there are three sports clubs, which we call \(A\), \(B\), and \(C\).

A student argues as follows:

“To find how many people attend at least one club, we can add the number of people in each club. However, students who attend all three clubs get counted three times. To fix this, we should subtract them twice. Therefore, the number of people who attend at least one club is \[\text{people in }A+\text{people in }B+\text{people in }C -2\times(\text{people in all three clubs}).\]”

Is this reasoning correct?

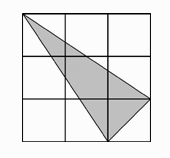
The diagram shows a triangle drawn on a square grid. The area of the shaded triangle is \(9~\text{cm}^2\). What is the area of one of the little squares of the grid?

The first \(2026\) prime numbers are multiplied. How many zeroes are at the end of this resulting number?

Three skiers—Alice, Bob, and Cynthia—compete in a downhill race. They begin skiing in the following order: first Cynthia, then Bob, and finally Alice.

Each skier starts with \(0\) points. Whenever one skier overtakes another during the race, the overtaking skier gains \(1\) point and the skier being overtaken loses \(1\) point.

At the end of the race, Alice crosses the finish line first, and Bob finishes with \(0\) points.

In what position does Cynthia finish?

On the Problemland Space Station, there are \(1000\) tonnes of air, of which \(99\%\) is oxygen. After an unfortunate asteroid impact, some of the air is vented into space. The hull is quickly repaired, and no further loss occurs.

Afterward, measurements reveal that oxygen now makes up only \(98\%\) of the remaining air, and that only oxygen was lost during the incident.

How many tonnes of oxygen remain on the space station?