Problems

Prove that under a homothety transformation, a circle is transformed into another circle. Consider all possible cases of \(k\): \(k<0, 0<k \leq 1, 1\leq k\).

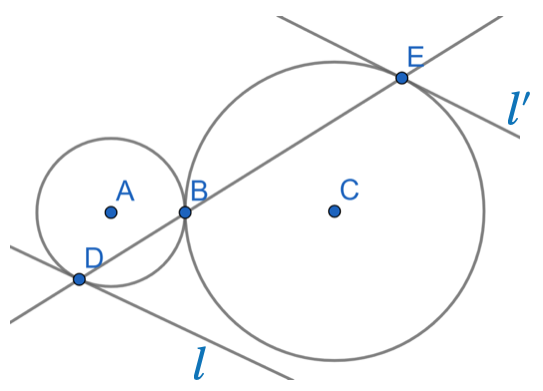
Two circles with centres \(A\) and \(C\) are tangent at the point \(B\). The segment \(DE\) passes through the point \(B\). Prove that the tangent lines \(l\) and \(l'\) passing through the points \(D\) and \(E\) respectively, are parallel.

Let \(ABCD\) be a square, a point \(I\) a random point on the plane. Consider the four points, symmetric to \(I\) with respect to the midpoints of \(AB, BC, CD, AD\). Prove that these new four points are vertices of a square.
In case you need a refresher, we say that a point \(X'\) is symmetric to a point \(X\) with respect to a point \(M\) if \(M\) is the midpoint of the segment \(XX'\).

Replace the stars with positive whole numbers so that \[\frac{1}{*}+\frac{1}{*}=\frac{7}{48}.\]

Let \(ABCD\) be a quadrilateral whose diagonals intersect at a point \(E\).

Consider the four triangles \(ABE\), \(BCE\), \(CDE\), and \(ADE\). For each triangle, draw its medians, and let \(K\), \(J\), \(M\), and \(L\) be the points where the medians intersect in the triangles \(ABE\), \(BCE\), \(CDE\), and \(ADE\), respectively.

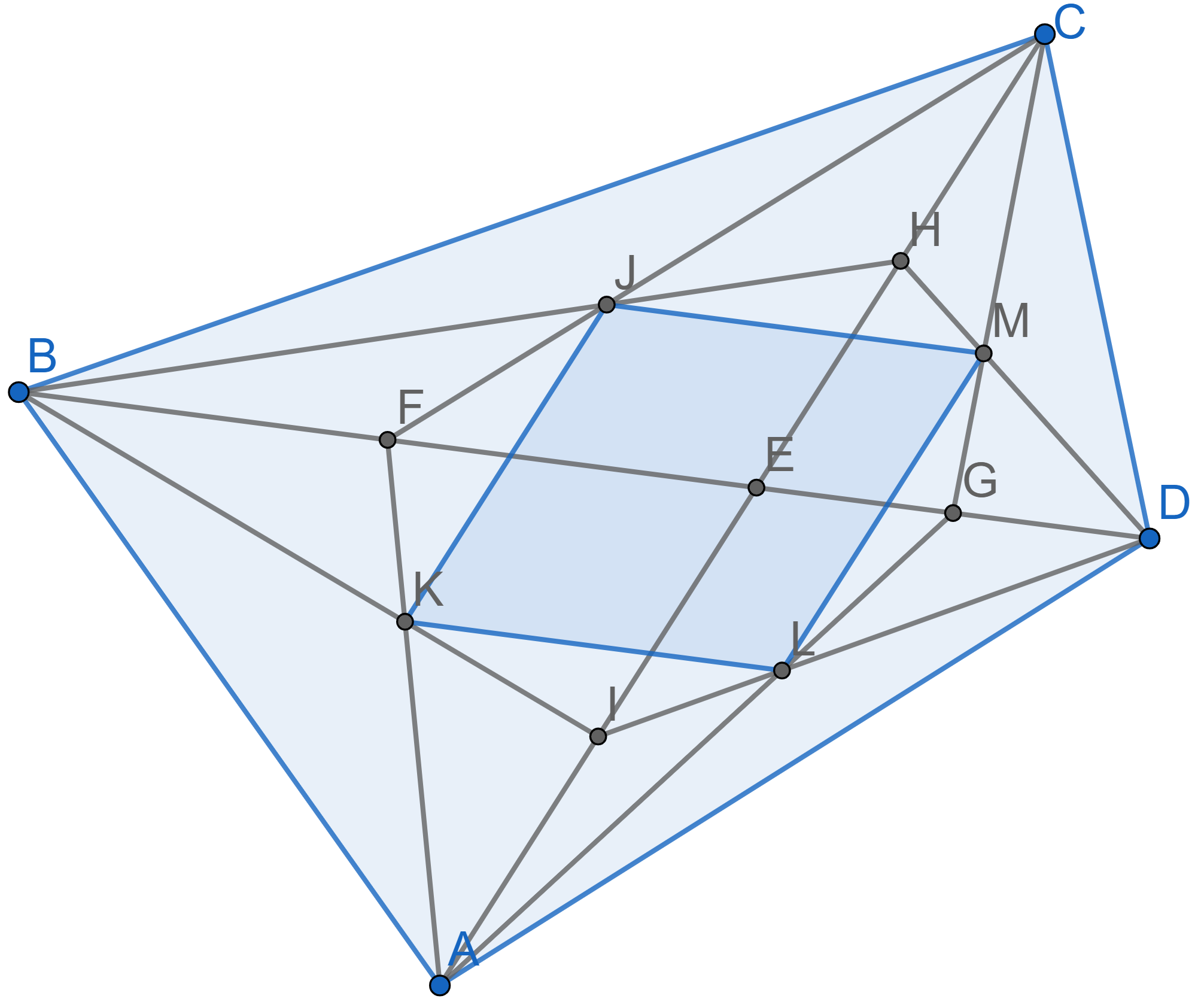
Prove that the quadrilateral \(KJML\) is a parallelogram.

You may wish to use the fact that the point of intersection of the medians of any triangle divides each median in the ratio \(2:1\), counting from the vertex, but if you use this fact, you should prove it.

At the Oscar Awards 2025, 5 films were nominated for Best Production Design and 5 films were nominated for Best Cinematography. In fact, 3 films were nominated for both categories. What is the total number of films nominated for these two categories?

150 young adults were asked how they commuted to work. 125 said they took the underground and 93 said they cycled. Of all the people interviewed, 72 said they both cycled and took the underground. How many people do not cycle and do not take the underground?

Show that there are no more than 269 prime numbers less than or equal to 1000.

200 people were asked if they drank one of the following beverages regularly: tea, coffee and beer. 165 people said they drank at least one of these beverages. Funnily, for every choice of a pair of beverages, exactly 122 people said they drank at least one beverage out of the pair. The even stranger fact was that for each choice of a beverage, exactly 73 people admitted to drinking it.

How many people drink all three beverages?

Each student chooses at least one from the \(n\) different modules offered at a university. Let us number these modules as \(1,2,3,\dots,n\). For each natural number \(1\leq k\leq n\), we denote the number of students choosing the modules \(i_1,\dots,i_k\) by \(S(i_1,\dots,i_k)\). Give a formula for the number of students in terms of the numbers \(S(i_1,\dots,i_k)\).

As an example, if \(n = 5\), \(k=3\) and we look at \(i_1 = 4,i_2 = 2, i_3 =1\), then \(S(i_1,i_2,i_3) = S(4,2,1)\) is the number of students picking the modules \(1,2,4\).