Problems
The king made a test for the future groom of his daughter. He put the princess in one of three rooms, a tiger in the other, and left the last room empty. It is known that the sign on the door where the princess is sitting is true, where the tiger is – it is false, and nothing is known about the sign on the third room. The tablets are as follows:
1 – room 3 is empty
2 – the tiger is in room 1
3 – this room is empty
Can the prince correctly guess the room with the princess?
a) A 1 or a 0 is placed on each vertex of a cube. The sum of the 4 adjacent vertices is written on each face of the cube. Is it possible for each of the numbers written on the faces to be different?
b) The same question, but if 1 and \(-1\) are used instead.
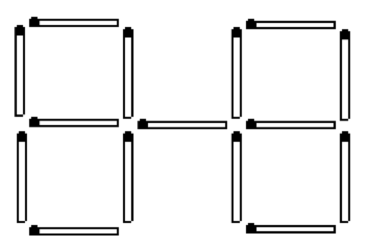
a) In the construction in the figure, move two matches so that there are five identical squares created. b) From the new figure, remove 3 matches so that only 3 squares remain.
How many squares are shown in the picture?

Gerard says: the day before yesterday I was 10 years old, and next year I will turn 13. Can this be?
We call a natural number “amazing” if it has the form \(a^b + b^a\) (where \(a\) and \(b\) are natural numbers). For example, the number 57 is amazing, since \(57 = 2^5 + 5^2\). Is the number 2006 amazing?
Homework. Cut a hole in an exercise book of a size so that you yourself can climb through it.
a) In how many ways can Dima paint five Christmas trees in silver, green and blue colours, if the amount of paint is unlimited, and he paints each tree in only one colour?
b) Dima has five baubles: a red, a green, a yellow, a blue and a gold one. In how many ways can he decorate five Christmas trees with them, if he needs to put exactly one bauble on each tree?
c) What about if he can hang several baubles on one Christmas tree (and all of the baubles have to be used)?
A toddler has \(25\) lego pieces in a box:
In how many ways are there to choose three pieces to play with?
In how many ways can he choose three pieces for the foundation, main walls and roof? Note that the order is important.
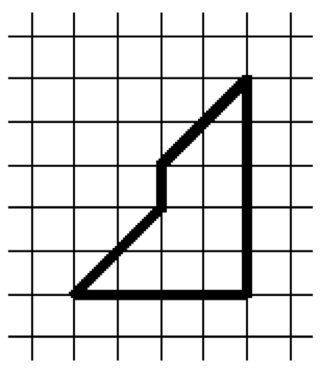
Cut the shape (see the figure) into two identical pieces (coinciding when placed on top of one another).