Problems
A toddler has \(25\) lego pieces in a box:
In how many ways are there to choose three pieces to play with?
In how many ways can he choose three pieces for the foundation, main walls and roof? Note that the order is important.
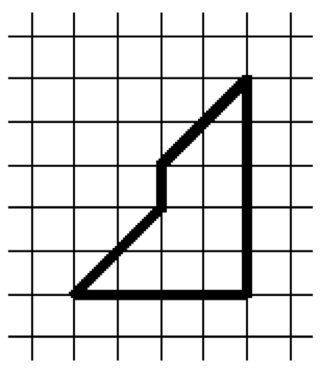
Cut the shape (see the figure) into two identical pieces (coinciding when placed on top of one another).
Gabby is standing on a river bank. She has two clay jars: one – for 5 litres, and about the second Gabby remembers only that it holds either 3 or 4 litres. Help Gabby determine the capacity of the second jar. (Looking into the jar, you cannot figure out how much water is in it.)
In the garden of Sandra and Lewis 2006 rose bushes were growing. Lewis watered half of all the bushes, and Sandra watered half of all the bushes. At the same time, it turned out that exactly three bushes, the most beautiful, were watered by both Sandra and Lewis. How many rose bushes have not been watered?
In a burrow there is a family of 24 mice. Every night exactly four of them are sent to the warehouse for cheese.
Could it occur that at some point in time each mouse went to the warehouse with every other mouse exactly one time?
In a physics club, the teacher created the following experiment. He spread out 16 weights of weight 1, 2, 3, ..., 16 grams onto weighing scales, so that one of the bowls outweighed the other. Fifteen students in turn left the classroom and took with them one weight each, and after each student’s departure, the scales changed their position and outweighed the opposite bowl of the scales. What weight could remain on the scales?
Solve the equation: \(|x-2005| + |2005-x|=2006\).
There is a \(5\times 9\) rectangle drawn on squared paper. In the lower left corner of the rectangle is a button. Kevin and Sophie take turns moving the button any number of squares either to the right or up. Kevin goes first. The winner is the one who places the button in upper right corner. Who would win, Kevin or Sophie, by using the right strategy?
Solve the equation: \[x + \frac{x}{x} + \frac{x}{x+\frac{x}{x}} = 1\]
Between them, Jennifer and Alex shared the money they made from running a lemonade stand. Jennifer thought: “If I took \(40\%\) more money then Alex’s share would decrease by \(60\%\)”. How would Alex’s share of the profits change if Jennifer took \(50\%\) more money for herself?