Problems

Does there exist a function \(f (x)\) defined for all \(x \in \mathbb{R}\) and for all \(x, y \in \mathbb{R}\) satisfying the inequality \(| f (x + y) + \sin x + \sin y | < 2\)?

We call a number \(x\) rational if it can be represented as \(x=\frac{p}{q}\) for coprime integers \(p\) and \(q\). Otherwise we call the number irrational.
Non-zero numbers \(a\) and \(b\) satisfy the equality \(a^2b^2 (a^2b^2 + 4) = 2(a^6 + b^6)\). Prove that at least one of them is irrational.

Prove that in any set of 117 unique three-digit numbers it is possible to pick 4 non-overlapping subsets, so that the sum of the numbers in each subset is the same.

A target consists of a triangle divided by three families of parallel lines into 100 equilateral unit triangles. A sniper shoots at the target. He aims at a particular equilateral triangle and either hits it or hits one of the adjacent triangles that share a side with the one he was aiming for. He can see the results of his shots and can choose when to stop shooting. What is the largest number of triangles that the sniper can guarantee he can hit exactly 5 times?

Can the cells of a \(5 \times 5\) board be painted in 4 colours so that the cells located at the intersection of any two rows and any two columns are painted in at least three colours?

The real numbers \(x\) and \(y\) are such that for any distinct prime odd \(p\) and \(q\) the number \(x^p + y^q\) is rational. Prove that \(x\) and \(y\) are rational numbers.

Is it possible to arrange the numbers 1, 2, ..., 60 in a circle in such an order that the sum of every two numbers, between which lies one number, is divisible by 2, the sum of every two numbers between which lie two numbers, is divisible by 3, the sum of every two numbers between which lie six numbers, is divisible by 7?

The functions \(f (x) - x\) and \(f (x^2) - x^6\) are defined for all positive \(x\) and increase. Prove that the function

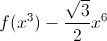
also increases for all positive \(x\).

The sum of the positive numbers \(a, b, c\) is \(\pi / 2\). Prove that \(\cos a + \cos b + \cos c > \sin a + \sin b + \sin c\).

The circles \(\sigma_1\) and \(\sigma_2\) intersect at points \(A\) and \(B\). At the point \(A\) to \(\sigma_1\) and \(\sigma_2\), respectively, the tangents \(l_1\) and \(l_2\) are drawn. The points \(T_1\) and \(T_2\) are chosen respectively on the circles \(\sigma_1\) and \(\sigma_2\) so that the angular measures of the arcs \(T_1A\) and \(AT_2\) are equal (the arc value of the circle is considered in the clockwise direction). The tangent \(t_1\) at the point \(T_1\) to the circle \(\sigma_1\) intersects \(l_2\) at the point \(M_1\). Similarly, the tangent \(t_2\) at the point \(T_2\) to the circle \(\sigma_2\) intersects \(l_1\) at the point \(M_2\). Prove that the midpoints of the segments \(M_1M_2\) are on the same line, independent of the positions of the points \(T_1, T_2\).