We solve problems

Problems Number Theory Divisibility Divisibility rules Divisibility tests for 3 and 9 Methods Proof by contradiction

Does there exist a natural number which, when divided by the sum of its digits, gives a quotient and remainder both equal to the number 2011?

Problem #PRU-116087

Problems Geometry Plane geometry Triangles Similar triangles Circles Tangent lines and tangent circles Tangent lines to circles

15–16 4.0

Three circles are constructed on a triangle, with the medians of the triangle forming the diameters of the circles. It is known that each pair of circles intersects. Let \(C_{1}\) be the point of intersection, further from the vertex \(C\), of the circles constructed from the medians \(AM_{1}\) and \(BM_{2}\). Points \(A_{1}\) and \(B_{1}\) are defined similarly. Prove that the lines \(AA_{1}\), \(BB_{1}\) and \(CC_{1}\) intersect at the same point.

Problem #PRU-116142

Problems Number Theory Equations in integer numbers

11–13 2.0

In a herd consisting of horses and camels (some with one hump and some with two) there are a total of 200 humps. How many animals are in the herd, if the number of horses is equal to the number of camels with two humps?

Problem #PRU-116145

Problems Algebra Algebraic inequalities and systems of inequalities Linear inequalites and systems of inequalities Discrete Mathematics Set theory and logic Logic and set theory

12–14 2.0

Of the four inequalities \(2x > 70\), \(x < 100\), \(4x > 25\) and \(x > 5\), two are true and two are false. Find the value of \(x\) if it is known that it is an integer.

Problem #PRU-116208

Problems Discrete Mathematics Algorithm Theory Balance puzzles

11–13 2.0

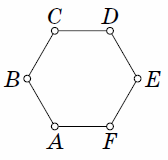
At the vertices of the hexagon \(ABCDEF\) (see Fig.) There were 6 identical balls: at \(A\) – one with mass 1 g, at \(B\) – 2 g, ..., at \(F\) – 6 g. Callum changed the places of two balls in opposite vertices. A set of weighing scales with 2 plates is available, which let you know which plate contains the balls of greater mass. How, in one weighing, can it be determined which balls were rearranged?

Problem #PRU-116256

Problems Geometry Solid geometry Visual geometry in space

11–13 2.0

Mark has 1000 identical cubes, each of which has one pair of opposite faces which are coloured white, another pair which are blue and a third pair that are red. He made a large \(10 \times 10 \times 10\) cube from them, joining cubes to one another which have the same coloured faces. Prove that the large cube has a face which is solidly one colour.

Problem #PRU-116278

Problems Methods Examples and counterexamples. Constructive proofs Pigeonhole principle Pigeonhole principle (other)

13–14 4.0

Two ants crawled along their own closed route on a \(7\times7\) board. Each ant crawled only on the sides of the cells of the board and visited each of the 64 vertices of the cells exactly once. What is the smallest possible number of cell edges, along which both the first and second ants crawled?

Problem #PRU-116301

Problems Geometry Plane geometry Geometrical inequalities Area inequalities Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.) Area

13–14 4.0

101 random points are chosen inside a unit square, including on the edges of the square, so that no three points lie on the same straight line. Prove that there exist some triangles with vertices on these points, whose area does not exceed 0.01.

Problem #PRU-116406

Problems Algebra and arithmetic Arithmetics. Mental maths

13–14 2.0

In six baskets there are pears, plums and apples. The number of plums in each basket is equal to the total number of apples in the other baskets. The number of apples in each basket is equal to the total number of pears in the other baskets. Prove that the total number of fruits is divisible by 31.

Problem #PRU-116430

Problems Algebra Surds. Rational powers Irrational inequalities.

14–16 2.0

Solve the following inequality: \(x+y^2 +\sqrt{x-y^2-1} \leq 1\).