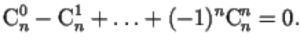Problems
Solve the equation \(3x + 5y = 7\) in integers. Make sure that you’ve found all integer solutions.
Determine all integer solutions of the equation \(3x - 12y = 7\).
Determine all the integer solutions for the equation \(21x + 48y = 6\).
Solve the equations \(x^2 = 14 + y^2\) in integers.
Solve the equation with integers \(x^2 + y^2 = 4z - 1\).
Let \(p\) be a prime number, and \(a\) an integer number not divisible by \(p\). Prove that there is a positive integer \(b\) such that \(ab \equiv 1 \pmod p\).
How many ways can Susan choose 4 colours from 7 different ones?
On the plane, 10 points are marked so that no three of them lie on the same line. How many triangles are there with vertices at these points?
Prove that out of \(n\) objects an even number of objects can be chosen in \(2^{n-1}\) ways.