Problems
In the city where the Scattered Scientist lives, telephone numbers consist of 7 digits. The scientist easily remembers a phone number, if this number is a palindrome, that is, it is identical when read from left to right and from right to left. For example, the number 4435344 the scientist remembers easily, because this number is a palindrome. And the number 3723627 is not a palindrome, so the scientist does not remember this number easily. Find the probability that the scientist will remember the phone number of a new random acquaintance easily.
Ben is going to bend a square sheet of paper \(ABCD\). Ben calls the fold beautiful, if the side \(AB\) crosses the side \(CD\) and the four resulting rectangular triangles are equal. Before that, Jack selects a random point on the sheet \(F\). Find the probability that Ben will be able to make a beautiful fold through the point \(F\).
40% of adherents of some political party are women. 70% of the adherents of this party are townspeople. At the same time, 60% of the townspeople who support the party are men. Are the events “the adherent of the party is a townsperson” and “the adherent of party is a woman” independent?
The Scattered Scientist constructed a device consisting of a sensor and a transmitter. The average life expectancy of the sensor part is 3 years, the average lifetime of the transmitter is 5 years. Knowing the distribution of the lifetime of the sensor and the transmitter, the Scattered Scientist calculated that the average lifetime of the entire device is 3 years 8 months. Was the Scattered Scientist wrong in his calculations?
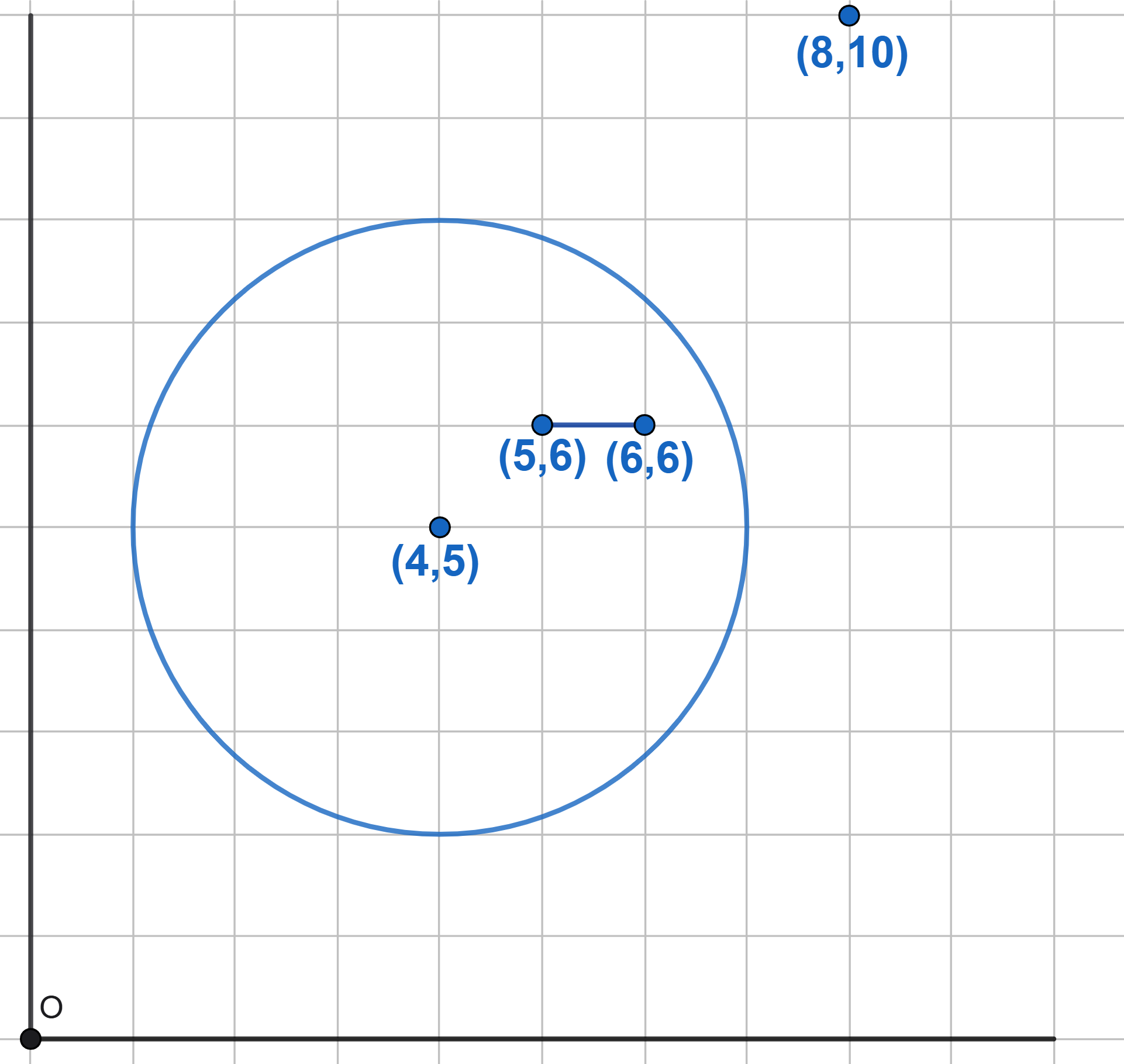
A fly crawls along a grid from the origin. The fly moves only along the lines of the integer grid to the right or upwards (monotonic wandering). In each node of the net, the fly randomly selects the direction of further movement: upwards or to the right. Find the probability that at some point:
a) the fly will be at the point \((8, 10)\);
b) the fly will be at the point \((8, 10)\), along the line passing along the segment connecting the points \((5, 6)\) and \((6, 6)\);
c) the fly will be at the point \((8, 10)\), passing inside a circle of radius 3 with center at point \((4, 5)\).
In a numerical set of \(n\) numbers, one of the numbers is 0 and another is 1.
a) What is the smallest possible variance of such a set of numbers?
b) What should be the set of numbers for this?
The television game “What? Where? When?” consists of a team of “experts” trying to solve 13 questions that are thought up and sent in by the viewers of the programme. Envelopes with the questions are selected in turn in random order with the help of a spinning top with an arrow. If the experts answer correctly, they earn a point, and if they answer incorrectly, the viewers get one point. The game ends as soon as one of the teams scores 6 points. The probability of the team of experts winning in one round is 0.6 and there can be no draws. Currently, the experts are losing 3 to 4. Find the probability that the experts will still win.
A fly moves from the origin only to the right or upwards along the lines of the integer grid (a monotonic wander). In each node of the net, the fly randomly selects the direction of further movement: upwards or to the right.
a) Prove that sooner or later the fly will reach the point with abscissa 2011.
b) Find the mathematical expectation of the ordinate of the fly at the moment when the fly reached the abscissa 2011.
The point \(O\), lying inside the triangle \(ABC\), is connected by segments with the vertices of the triangle. Prove that the variance of the set of angles \(AOB\), \(AOC\) and \(BOC\) is less than a) \(10\pi ^2/27\); b) \(2\pi ^2/9\).
King Arthur has two equally wise advisers – Merlin and Percival. Each of them finds the correct answer to any question with probability \(p\) or an incorrect answer, with probability \(q = 1 - p\).
If both counsellors say the same thing, the king listens to them. If they say opposite things, then the king chooses a solution by tossing a coin.
One day, Arthur thought about why he had two advisers, would one not be enough? Then the king called for his counsellors and said:
“It seems to me that the probability of making the right solutions will not decrease if I keep one adviser and listen to him. If so, I must fire one of you. If not, I’ll leave it as it is. Tell me, should I fire one of you?”.
“Who exactly are you going to fire, King Arthur?”, asked the advisers.
“If I make the solution to fire one of you, I will make a choice by tossing a coin”.
The advisers went to think about the answer. The advisors, we repeat, are equally wise, but not equally honest. Percival is very honest and will try to give the right answer, even if he faces dismissal. And Merlin, honest about everything else, in this situation decides to give such an answer with which the probability of his dismissal is as low as possible. What is the probability that Merlin will be fired?