Problems

On a calculator keypad, there are the numbers from 0 to 9 and signs of two actions (see the figure). First, the display shows the number 0. You can press any keys. The calculator performs the actions in the sequence of clicks. If the action sign is pressed several times, the calculator will only remember the last click.

a) The button with the multiplier sign breaks and does not work. The Scattered Scientist pressed several buttons in a random sequence. Which result of the resulting sequence of actions is more likely: an even number or an odd number?

b) Solve the previous problem if the multiplication symbol button is repaired.

On a Christmas tree, 100 light bulbs hang in a row. Then the light bulbs begin to switch according to the following algorithm: all are lit up, then after a second, every second light goes out, after another second, every third light bulb changes: if it was on, it goes out and vice versa. After another second, every fourth bulb switches, a second later – every fifth and so on. After 100 seconds the sequence ends. Find the probability that a light bulb straight after a randomly selected light bulb is on (bulbs do not burn out and do not break).

In the final of a contest of performances on March 8 two performances were left. In the first, $n$ pupils from the class 5A performed, and in the second – $n$ pupils of class 5B. At the play there were $2n$ mothers of all $2n$ students. The best performance is chosen by a vote by the mums. It is known that every mother, with a probability of $\frac{1}{2}$, votes for the best performance and with a probability of $\frac{1}{2}$ – for the performance in which her child participates.

a) Find the probability that the best performance will win with a majority of votes.

b) The same question, if more than two classes have reached the finals.

In honor of the March 8 holiday, a competition of performances was organized. Two performances reached the final. $N$ students of the 5th grade played in the first one and $n$ students of the 4th grade played in the second one. The performance was attended by $2n$ mothers of all $2n$ students. The best performance is chosen by a vote of the mothers. It is known that half of the mothers vote honestly, i.e. for the performance that was truly better and the mothers of the other half in any case vote for the performance in which their child participates.

a) Find the probability of the best performance winning by a majority of votes.

b) The same question but this time more than two performances made it to the final.

A sailor can only serve on a submarine if their height does not exceed 168 cm. There are four teams $A$, $B$, $C$ and $D$. All sailors in these teams want to serve on a submarine and have been rigorously selected. There remains the last selection round – for height.

In team $A$, the average height of sailors is 166 cm.

In team $B$, the median height of the sailors is 167 cm.

In team $C$, the tallest sailor has a height of 169 cm.

In team $D$, the mode of the height of the sailors is 167 cm.

In which team, can at least half of the sailors definitely serve on the submarine?

The length of the hypotenuse of a right-angled triangle is 3.

a) The Scattered Scientist calculated the dispersion of the lengths of the sides of this triangle and found that it equals 2. Was he wrong in the calculations?

b) What is the smallest standard deviation of the sides that a rectangular triangle can have? What are the lengths of its sides, adjacent to the right angle?

The mathematics teacher suggested changing the voting scheme at the performance competition. Currently, two groups compete in the final. In the first group, there are $n$ pupils from class 5A, and in the second, there are $n$ pupils from class 5B. $2n$ mothers of all $2n$ students attended the final of the competition. The best performance is chosen by the mothers voting. It is known that exactly half of the mothers vote honestly for the best performance, and the other half, in any case, vote for the performance in which her child participates (see problem number 65299). The teacher believes that it is necessary to choose a jury of $2m$ people $(2m\text{ensuremath}\le n)$ from all $2n$ mums at random. Find the probability that the best performance will win under such voting conditions.

A numerical set $x_1,\dots ,x_n$ is given. Consider the function $d(t)=\frac{mi{n}_{i=1,\dots ,n}|x_i-t|+ma{x}_{i=1,\dots ,n}|x_i-t|}{2}$.

a) Is it true that the function $d(t)$ takes the smallest value at a single point, for any set of numbers $x_1,\dots ,x_n$?

b) Compare the values of $d(c)$ and $d(m)$ where $c=\frac{mi{n}_{i=1,\dots ,n}{x}_i+ma{x}_{i=1,\dots ,n}{x}_i}{2}$ and $m$ is the median of the specified set.

James furiously cuts a rectangular sheet of paper with scissors. Every second he cuts a random piece by an unsystematic rectilinear cut into two parts.

a) Find the mathematical expectation of the number of sides of a polygon (made from a piece of paper) that James randomly picks up after an hour of such work.

b) Solve the same problem if at first the piece of paper had the form of an arbitrary polygon.

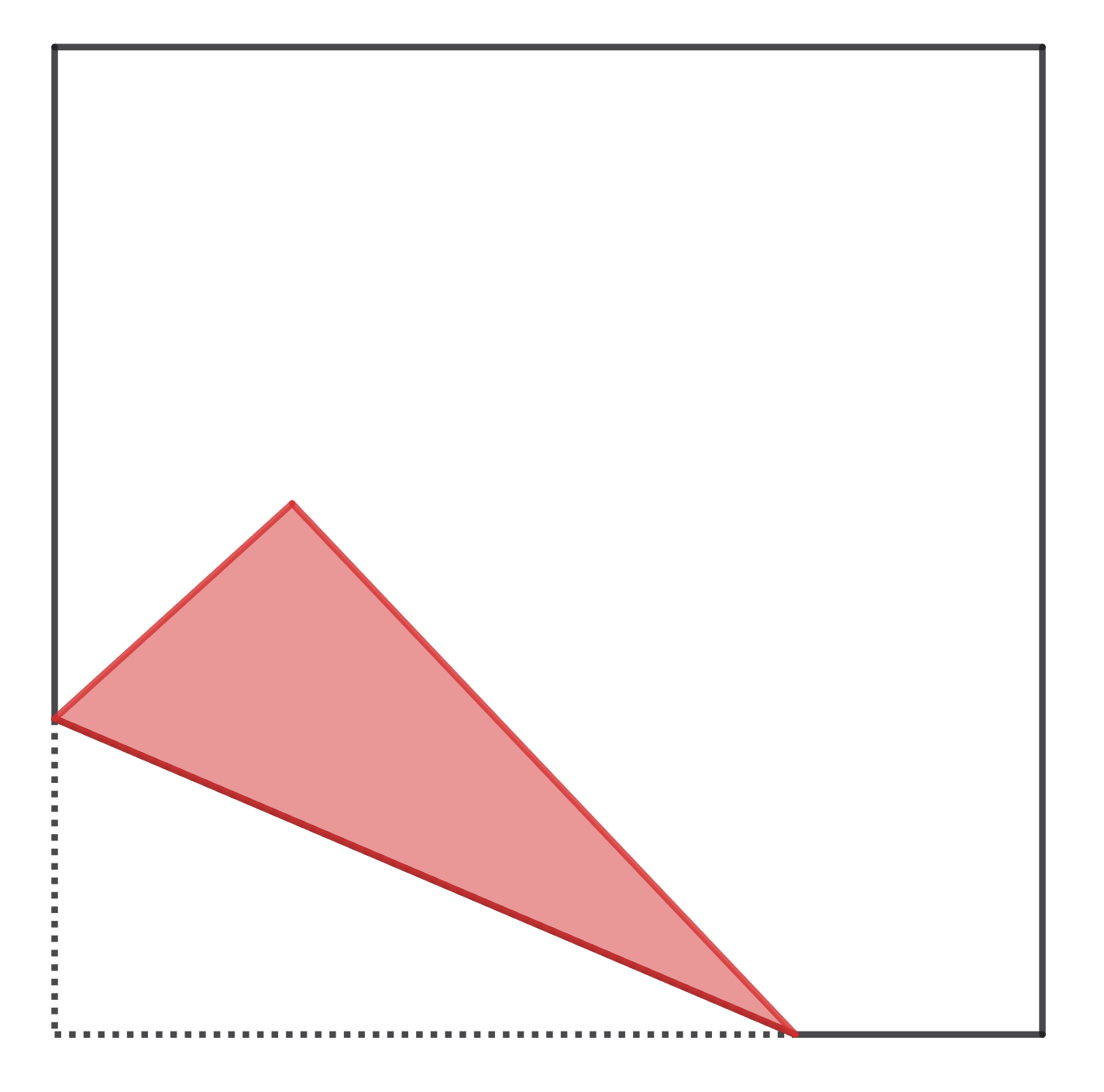
The upper side of a piece of square paper is white, and the lower one is red. In the square, a point F is randomly chosen. Then the square is bent so that one randomly selected vertex overlaps the point F. Find the mathematical expectation of the number of sides of the red polygon that appears.