Problems

An infinite sequence of digits is given. One may consider a finite set of consecutive digits and view it as a number in decimal expression, whose digits shall be read from left to right, as usual. Prove that, for any natural number \(n\) which is relatively prime with 10, you can choose a finite set of consecutive digits which gives you a multiple of \(n\).

Author: V.A. Popov

On the interval \([0; 1]\) a function \(f\) is given. This function is non-negative at all points, \(f (1) = 1\) and, finally, for any two non-negative numbers \(x_1\) and \(x_2\) whose sum does not exceed 1, the quantity \(f (x_1 + x_2)\) does not exceed the sum of \(f (x_1)\) and \(f (x_2)\).

a) Prove that for any number \(x\) on the interval \([0; 1]\), the inequality \(f (x_2) \leq 2x\) holds.

b) Prove that for any number \(x\) on the interval \([0; 1]\), the \(f (x_2) \leq 1.9x\) must be true?

The triangle \(C_1C_2O\) is given. Within it the bisector \(C_2C_3\) is drawn, then in the triangle \(C_2C_3O\) – bisector \(C_3C_4\) and so on. Prove that the sequence of angles \(\gamma_n = C_{n + 1}C_nO\) tends to a limit, and find this limit if \(C_1OC_2 = \alpha\).

A rectangular chocolate bar size \(5 \times 10\) is divided by vertical and horizontal division lines into 50 square pieces. Two players are playing the following game. The one who starts breaks the chocolate bar along some division line into two rectangular pieces and puts the resulting pieces on the table. Then players take turns doing the same operation: each time the player whose turn it is at the moment breaks one of the parts into two parts. The one who is the first to break off a square slice \(1\times 1\) (without division lines) a) loses; b) wins. Which of the players can secure a win: the one who starts or the other one?

What has a greater value: \(300!\) or \(100^{300}\)?

A quadrilateral is given; \(A\), \(B\), \(C\), \(D\) are the successive midpoints of its sides, \(P\) and \(Q\) are the midpoints of its diagonals. Prove that the triangle \(BCP\) is equal to the triangle \(ADQ\).

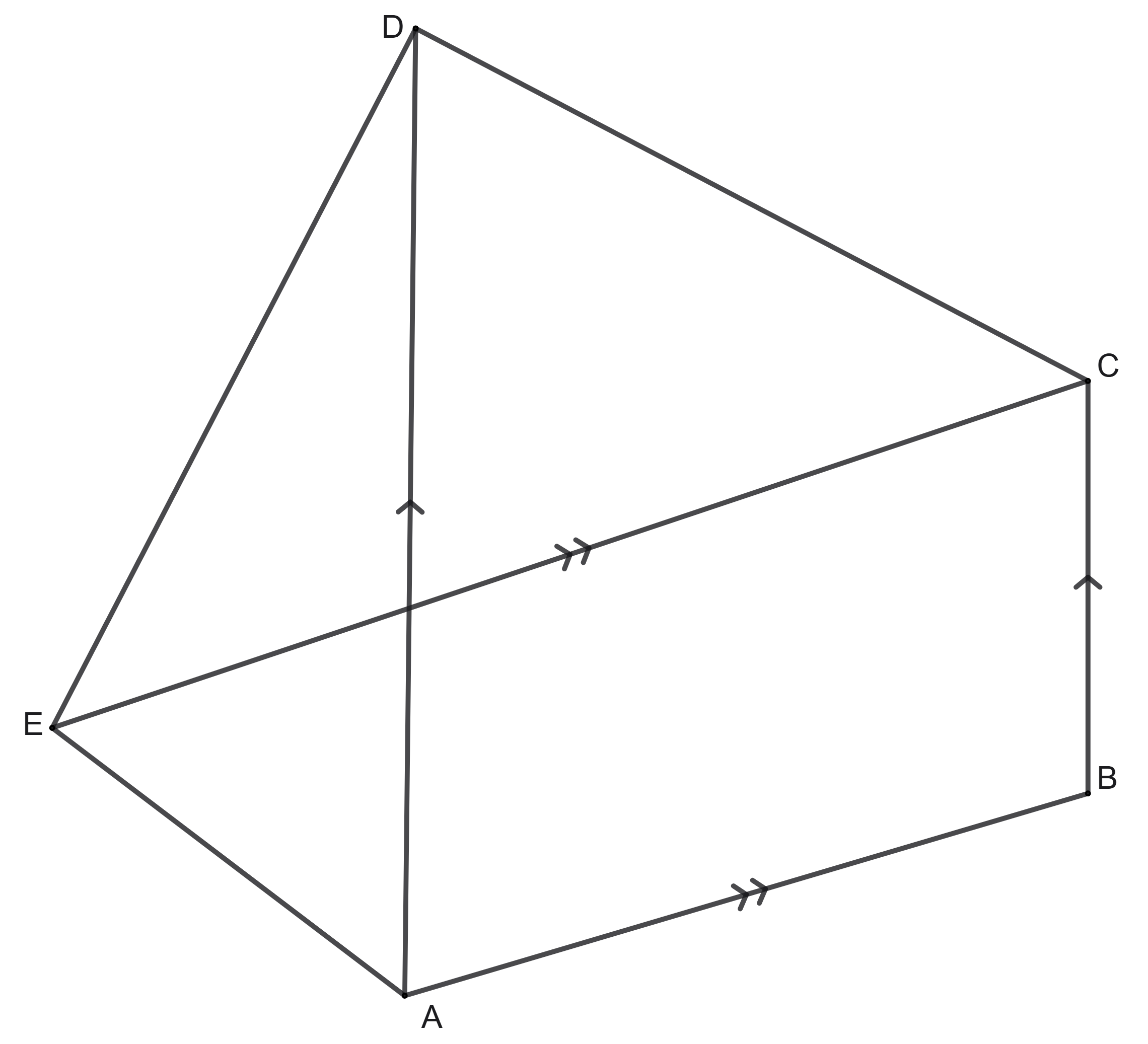
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.

Prove that, for any integer \(n\), among the numbers \(n, n + 1, n + 2, \dots , n + 9\) there is at least one number that is mutually prime with the other nine numbers.

How can you arrange the numbers \(5/177\), \(51/19\) and \(95/9\) and the arithmetical operators “\(+\)”, “\(-\)”, “\(\times\)” and “\(\div\)” such that the result is equal to 2006? Note: you can use the given numbers and operators more than once.

There are 13 weights, each weighing an integer number of grams. It is known that any 12 of them can be divided into two cups of weights, six weights on each one, which will come to equilibrium. Prove that all the weights have the same weight.