Problems
Long ago, in a galaxy far away, there was a planet of Liars and Truth-Tellers. Liars always tell lies, and Truth-Tellers always tell the truth. All the people on the planet look exactly the same, so you can’t tell who is who just by looking at them. In this problem sheet, we will explore some clever ways we can gather information from these aliens despite this difficulty.
Last weekend we held the verbal challenge and today we decided to demonstrate solutions of the most juicy problems.
Today we will focus on the study of Euclidean geometry of plane figures. Around 300 BCE a Greek mathematician Euclid developed a rigorous way to study plane geometry in his work Elements based on axioms (statement assumed to be correct) and theorems (statements deduced from axioms). The axioms of Euclidean Elements are the following:
For any two different points, there exists a line containing these two points, and this line is unique.
A straight line segment can be prolonged indefinitely.
A circle is defined by a point for its centre and a distance for its radius.
All right angles are equal.
For any line \(L\) and point \(P\) not on \(L\), there exists a line through \(P\) not meeting \(L\), and this line is unique.
In examples we deduce from the axioms above the following basic
principles:
1. The supplementary angles (angles "hugging" a straight line) add up to
\(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).
3. A line cutting two parallel lines cuts them at the same angles (these
are called corresponding angles).
4. In an isosceles triangle (which has two sides of equal lengths), the
two angles touching the third side are equal.
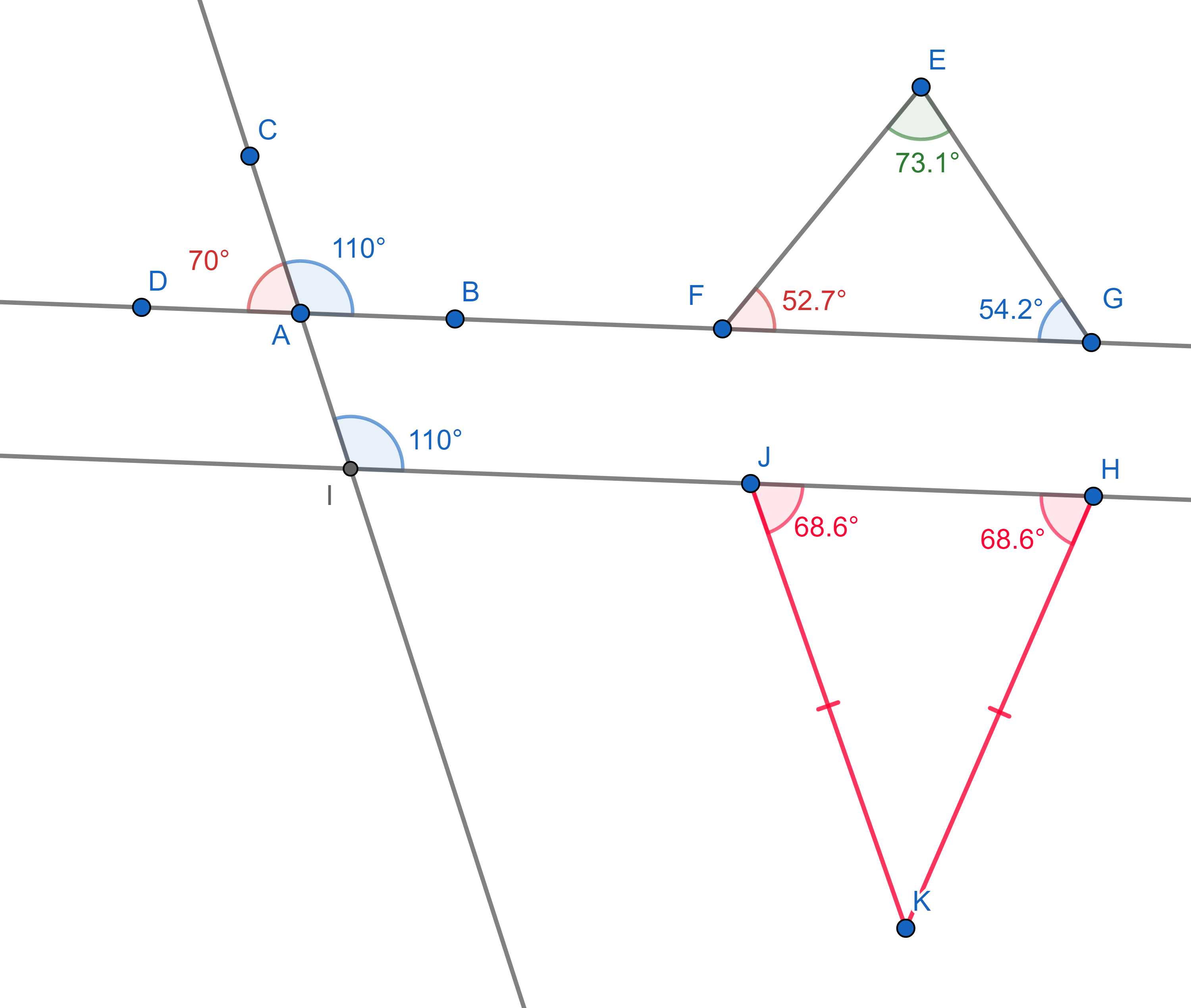
Let’s have a look at some examples of how to apply these axioms to prove geometric statements.
Consider a quadrilateral \(ABCD\). Choose a point \(E\) on side \(AB\). A line parallel to the diagonal \(AC\) is drawn through \(E\) and meets \(BC\) at \(F\). Then a line parallel to the other diagonal \(BD\) is drawn through \(F\) and meets \(CD\) at \(G\). And then a line parallel to the first diagonal \(AC\) is drawn through \(G\) and meets \(DA\) at \(H\). Prove the \(EH\) is parallel to the diagonal \(BD\).
Cut an arbitrary triangle into parts that can be used to build a triangle that is symmetrical to the original triangle with respect to some straight line (the pieces cannot be inverted, they can only be rotated on the plane).
The numbers from \(1\) to \(9\) are written in a row. Is it possible to write down the same numbers from \(1\) to \(9\) in a second row beneath the first row so that the sum of the two numbers in each column is an exact square?
On a Halloween night ten children with candy were standing in a row. In total, the girls and boys had equal amounts of candy. Each child gave one candy to each person on their right. After that, the girls had \(25\) more candy than they used to. How many girls are there in the row?
There are \(16\) cubes, each face of every cube is coloured yellow, black, or red (different cubes can be coloured differently). After looking at their colouring pattern, Pinoccio said that he could put all the cubes on the table in such a way that only the yellow color would be visible, on the next turn he could put the cubes in such a way that only the black color would be visible, and also he could put them in such a way that only the red color would be visible. Is there a colouring of the cubes such that he could tell the truth?
Alex writes natural numbers in a row: \(123456789101112...\) Counting from the beginning, in what places do the digits \(555\) first appear? For example, \(101\) first appears in the 10th, 11th and 12th places.
Find the representation of \((a+b)^n\) as the sum of \(X_{n,k}a^kb^{n-k}\) for general \(n\). Here by \(X_{n,k}\) we denote coefficients that depend only on \(k\) and \(n\).