Problems
A \(7 \times 7\) square was tiled using \(1 \times 3\) rectangular blocks in such a way that one of the squares has not been covered. Find all the squares that could be left without being covered.
Can you cover a \(13 \times 13\) square using \(2 \times 2\) and \(3 \times 3\) squares?
Is it possible to cover a \(10 \times 10\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.
Coloring is a very neat technique in problems involving boards since
it allows us to simplify the problem a great deal. The important part is
focusing on an adequate subset of the squares, however doing it with
colors is a lot easier.
The kinds of colorings can be very different and there is no general
rule for determining which one is going to solve the problem. There are
some colorings (such as a chessboard coloring) that are frequently used,
but the only way to learn how to use this technique is by solving
several problems of this style.
When the problem is related to pieces covering a certain figure, the
“good colorings” are those that yield an invariant associated with the
pieces. This can be the number of squares of one color they cover, the
number of colors they may use, some parity argument, etc. Coloring is
basically an illustrative way to describe invariants.
On a \(9\times 9\) board \(65\) bugs are placed in the centers of some of the squares. The bugs start moving at the same time and speed to a square that shares a side with the one they were in. When they reach the center of that square, they make a \(90\) degrees turn and keep walking (without leaving the board). Prove that at some moment of time there are two bugs in the same square. Note: When they turn it can be either to the right or to the left.
A \((2n - 1) \times (2n - 1)\) board is tiled with pieces of the following possible types:
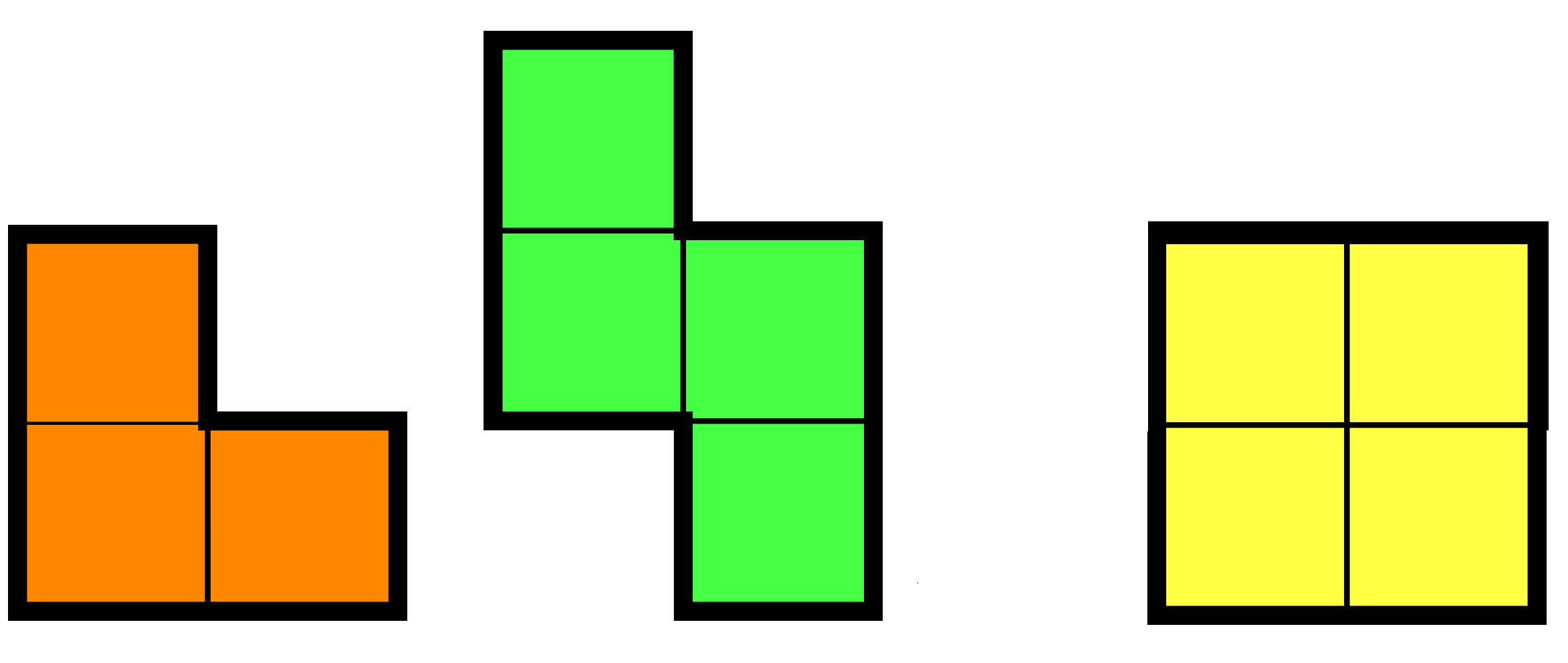
Prove that at least \(4n-1\) of the first type have been used.
In an \(n \times n\) board the squares are painted black or white in some way. Three of the squares in the corners are white and one is black. Show that there is a \(2\times 2\) square with an odd number of white unit squares.
On an \(8\times 8\) board there is a lamp in every square. Initially every lamp is turned off. In a move we choose a lamp and a direction (it can be the vertical direction or the horizontal one) and change the state of that lamp and all its neighbours in that direction. After a certain number of moves, there is exactly one lamp turned on. Find all the possible positions of that lamp.
In an \(5\times 5\) board one corner was removed. Is it possible to cover the remaining board with linear trominos (\(1\times 3\) blocks)?
One can hardly imagine modern life without numbers, but have you
wondered when and how the numbers were invented? It turns out people
started using numbers about \(42000\)
years BCE supposedly to mark the dates in calendar. But how do we
represent the numbers in writing? Well, there are two ways: examples of
the first abstract numeral systems are generally tallying
systems, the ones where the value or contribution of a digit
does not depend on its position, a good example is the famous Roman
numeral system: \(I\, V\, X\, L\, C\, D\,
M\), here a digit has only one value: \(I\) means one, \(X\) means ten and \(C\) a hundred. However, one might struggle
to express large numbers in Roman system.
Majority of ancient civilisations, Sumerian, Egyptian, Babylonian,
Chinese, Japanese, Indian used what is called positional numeral
systems, where the contribution of a digit to the value of a number is
the value of the digit multiplied by a factor determined by the position
of the digit. All these systems, even when invented independently, have
something in common, they are what is called "base-\(10\)".
Try to guess why do we use the decimal numeral system, which has exactly
\(10\) digits in our everyday use.
Because it does not actually have to be \(10\) digits, it could easily be \(3,8,16\), the binary system (with only
digits \(0\) and \(1\)) is used in all electronic devices,
since it is enough to represent any bit of information we might possibly
know.