Problems
\(CD\) is a chord of a circle with centre \(A\). The line \(CD\) is parallel to the tangent to the circle at the point \(B\). Prove that the triangle \(BCD\) is isosceles.
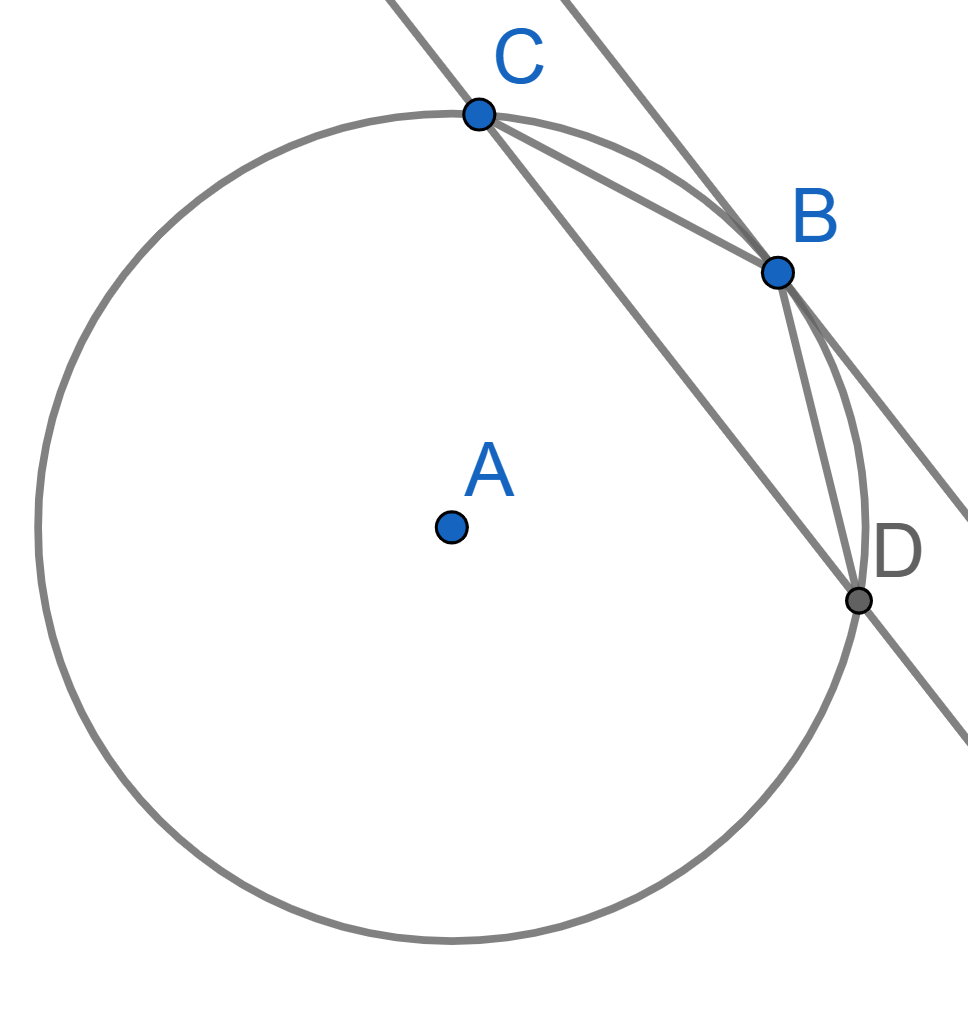
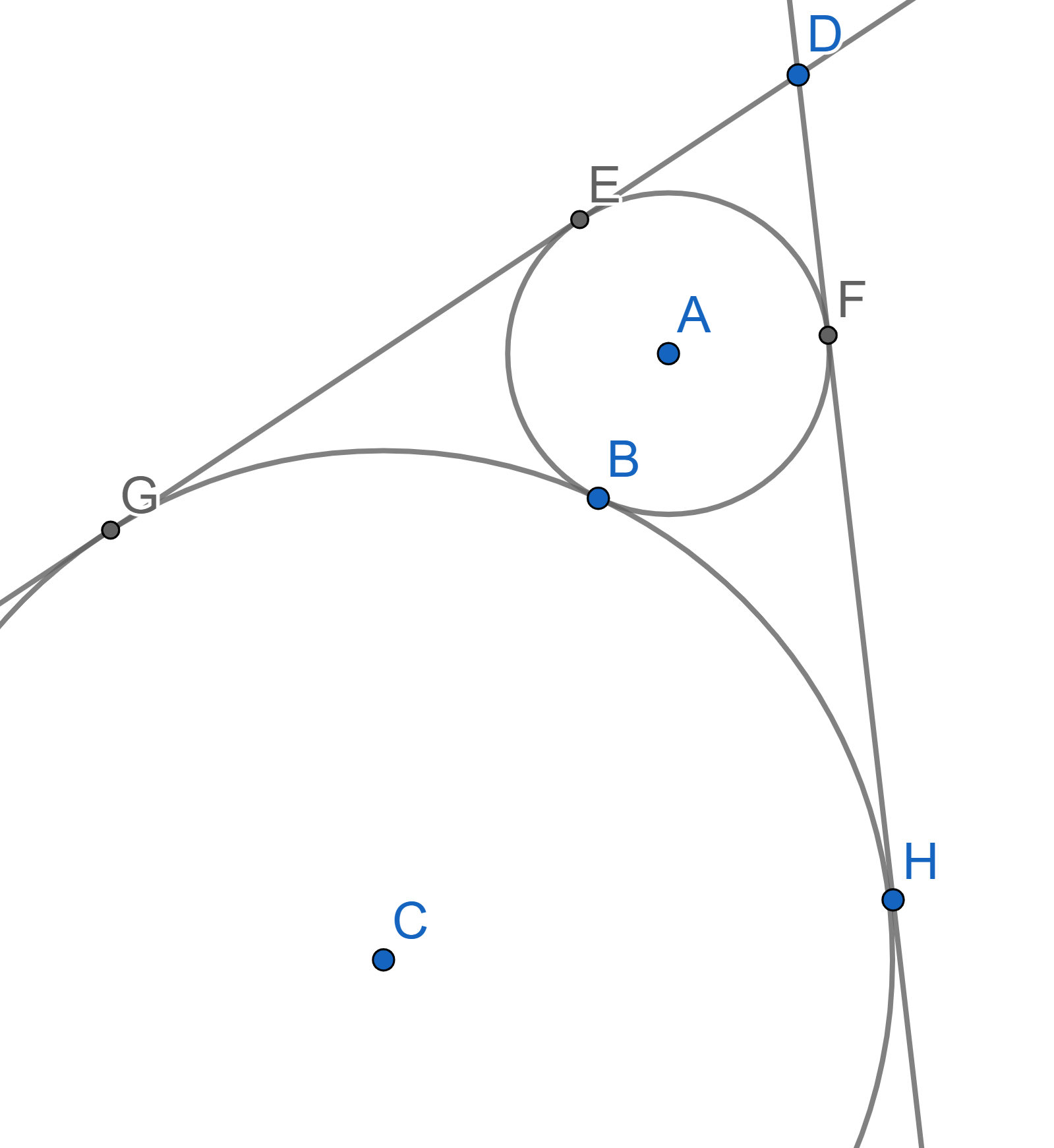
Four lines, intersecting at the point \(D\), are tangent to two circles with a common center \(A\) at the points \(C,F\) and \(B,E\). Prove that there exists a circle passing through all the points \(A,B,C,D,E,F\).
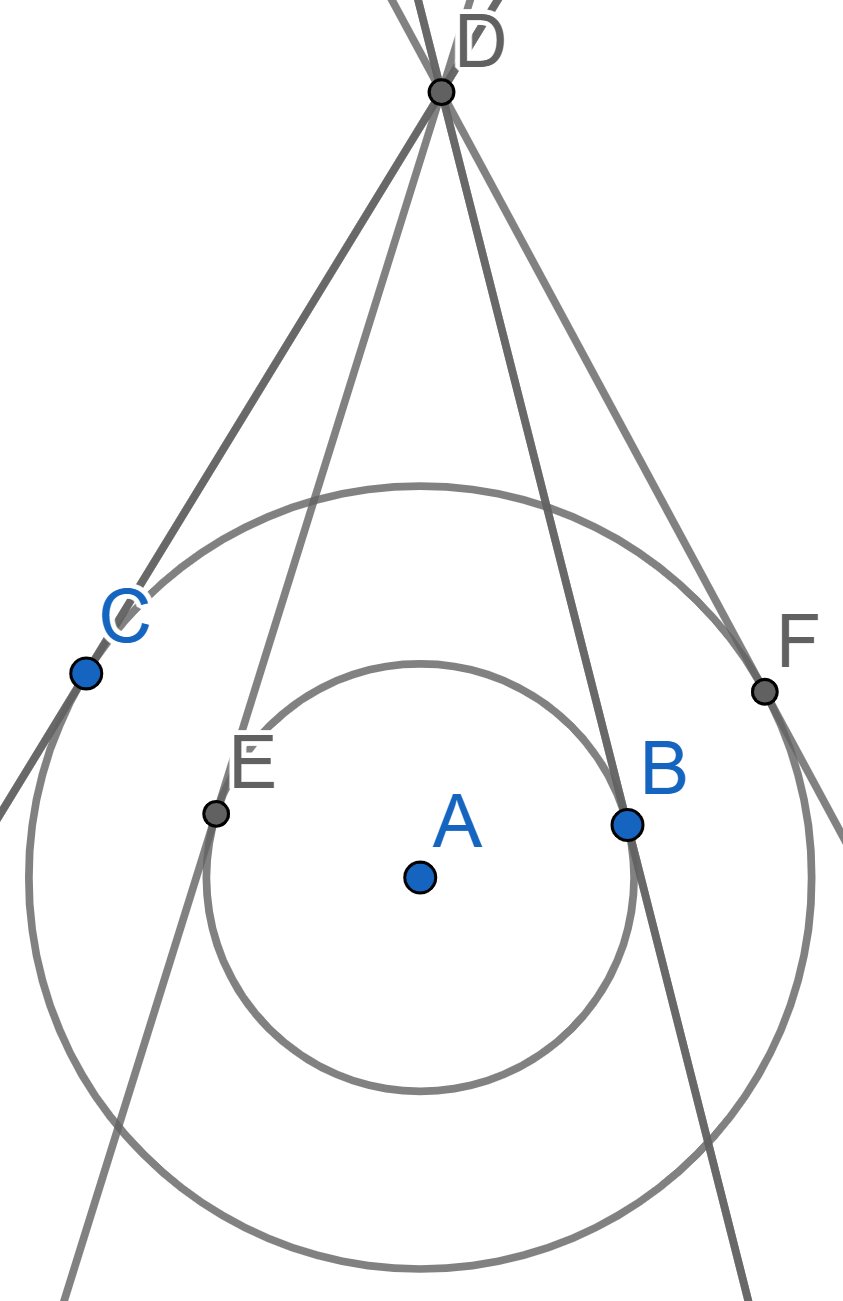
A circle with center \(A\) is inscribed into the triangle \(CDE\), so that all the sides of the triangle are tangent to the circle. We know the lengths of the segments \(ED=c, CD=a, EC=b\). The line \(CD\) is tangent to the circle at the point \(B\) - find the lengths of segments \(BD\) and \(BC\).
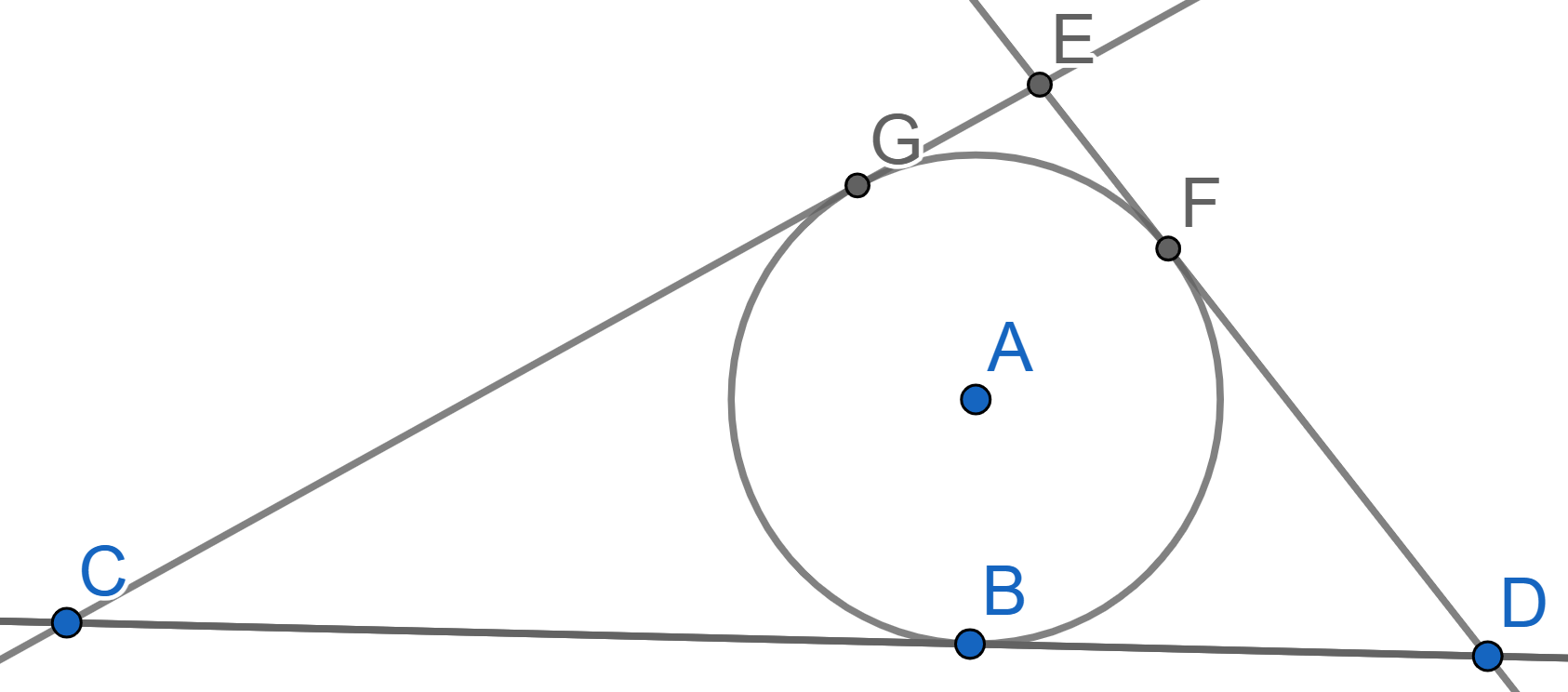
A circle with center \(A\) is tangent to all the sides of the quadrilateral \(FGHI\) at the points \(B,C,D,E\). Prove that \(FG+HI = GH+FI\).
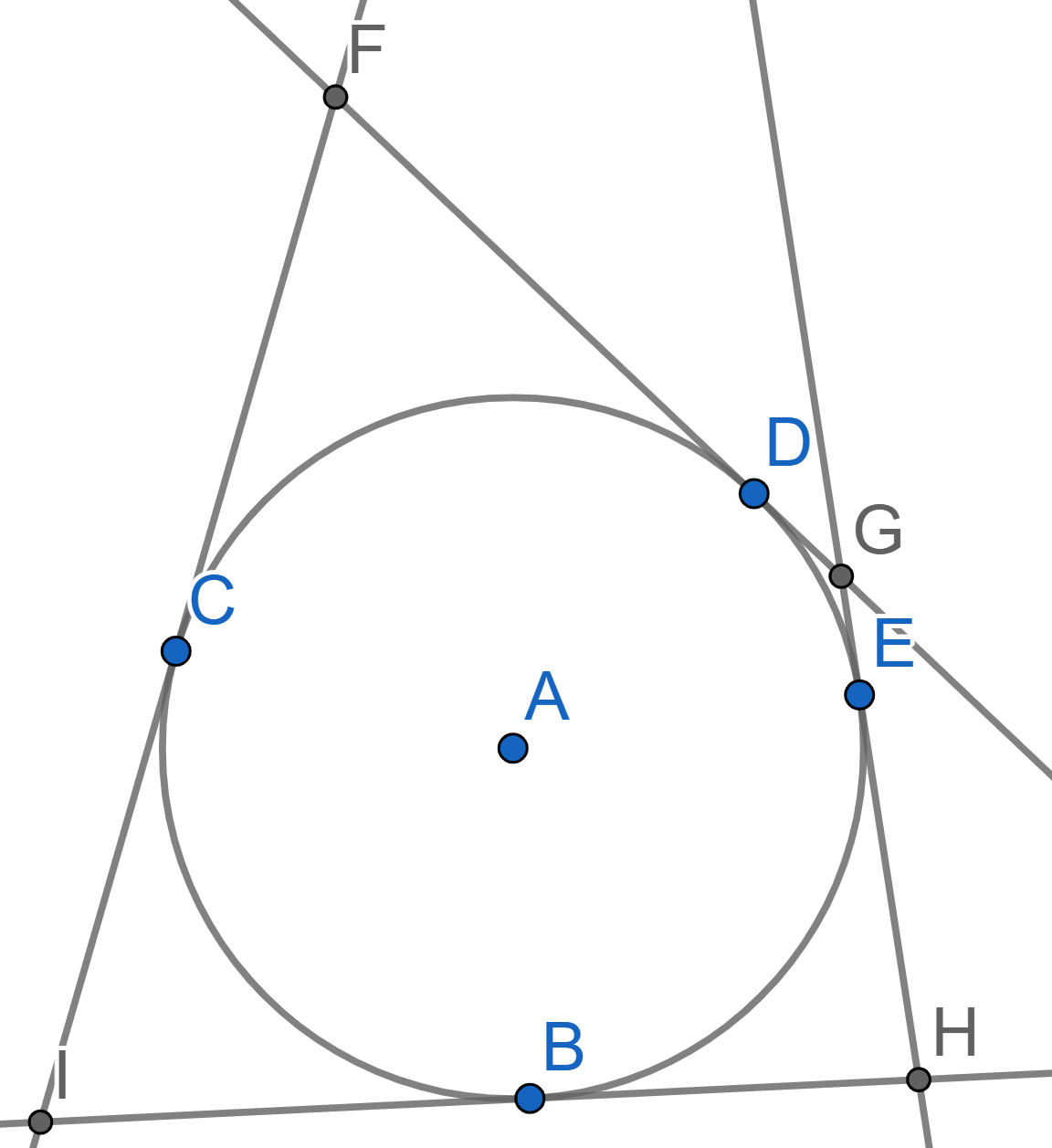
Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Both circles are tangent to the sides of an angle with vertex \(D\). It is known that the angle \(\angle EDF = 60^{\circ}\) and the radius of the smaller circle \(AF=5\). Find the radius of the large circle.
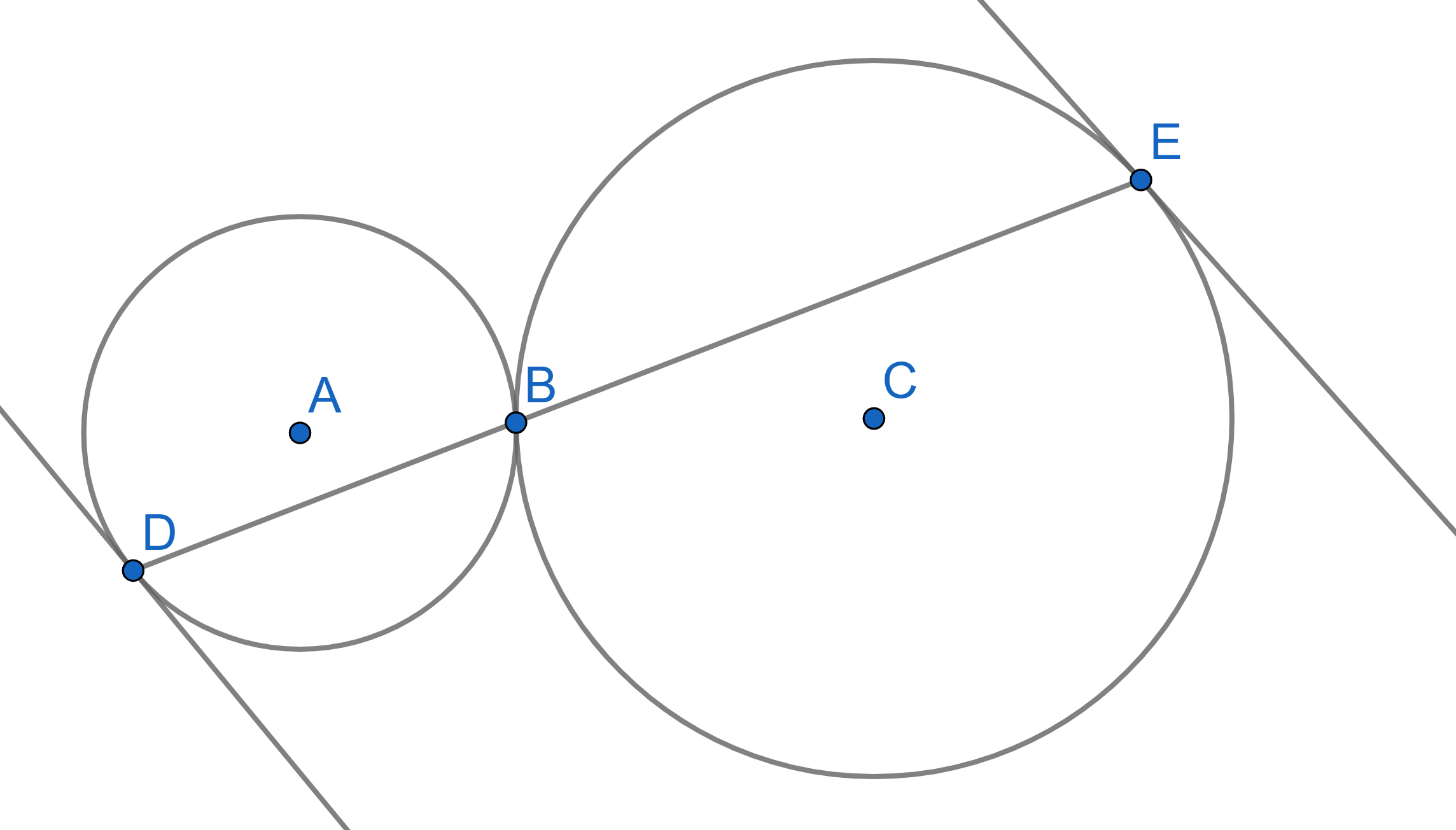
Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Two points \(D\) and \(E\) are chosen on the circles in such a way that a segment \(DE\) passes through the point \(B\). Prove that the tangent line to one circle at the point \(D\) is parallel to the tangent line to the other circle at the point \(E\).
Is it true that if \(a\) is a positive number, then \(a^2 \ge a\)? What about \(a^2 +1 \ge a\)?
Show for positive \(a\) and \(b\) that \(a^2 +b^2 \ge 2ab\).
Is it true that if \(b\) is a positive number, then \(b^3 + b^2 \ge b\)? What about \(b^3 +1 \ge b\)?
Show that if \(a\) is positive, then \(1+a \ge 2 \sqrt{a}\).