Problems
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.
Draw how Robinson Crusoe should arrange pegs and ropes so that his goat grazes in the shape of a hexagon. The hexagon doesn’t need to be regular.
Robinson Crusoe’s goat is tied to a single peg with one rope. Draw how Robinson should arrange pegs, ropes, a sliding ring, and a wolf so that the goat grazes in the shape of a half-circle.
One day, Robinson found a wolf in the island. He took the wolf with him and tied it with a rope to a peg. Robinson noticed that the goat would not graze anywhere that the wolf could reach. How could Robinson arrange both animals with pegs and ropes so that the goat can only graze in the shape of a waning moon? (see picture below)

Draw how Robinson Crusoe should arrange pegs, ropes, and a wolf so that the goat grazes grass in the shape of a half-ring.
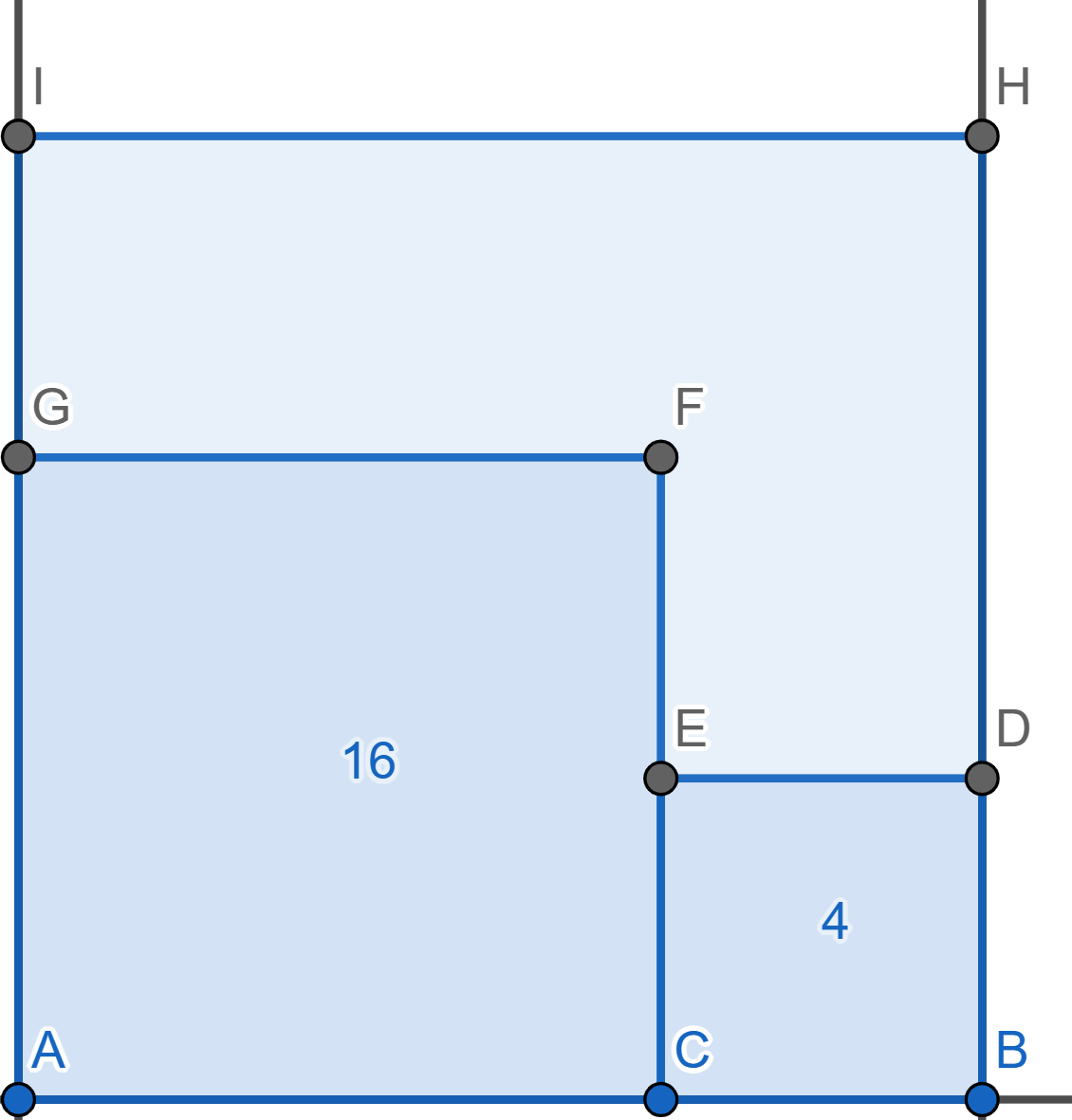
Each number denotes the area of a rectangle it is written into. What is the area of the last rectangle? (That is, the yellow one)
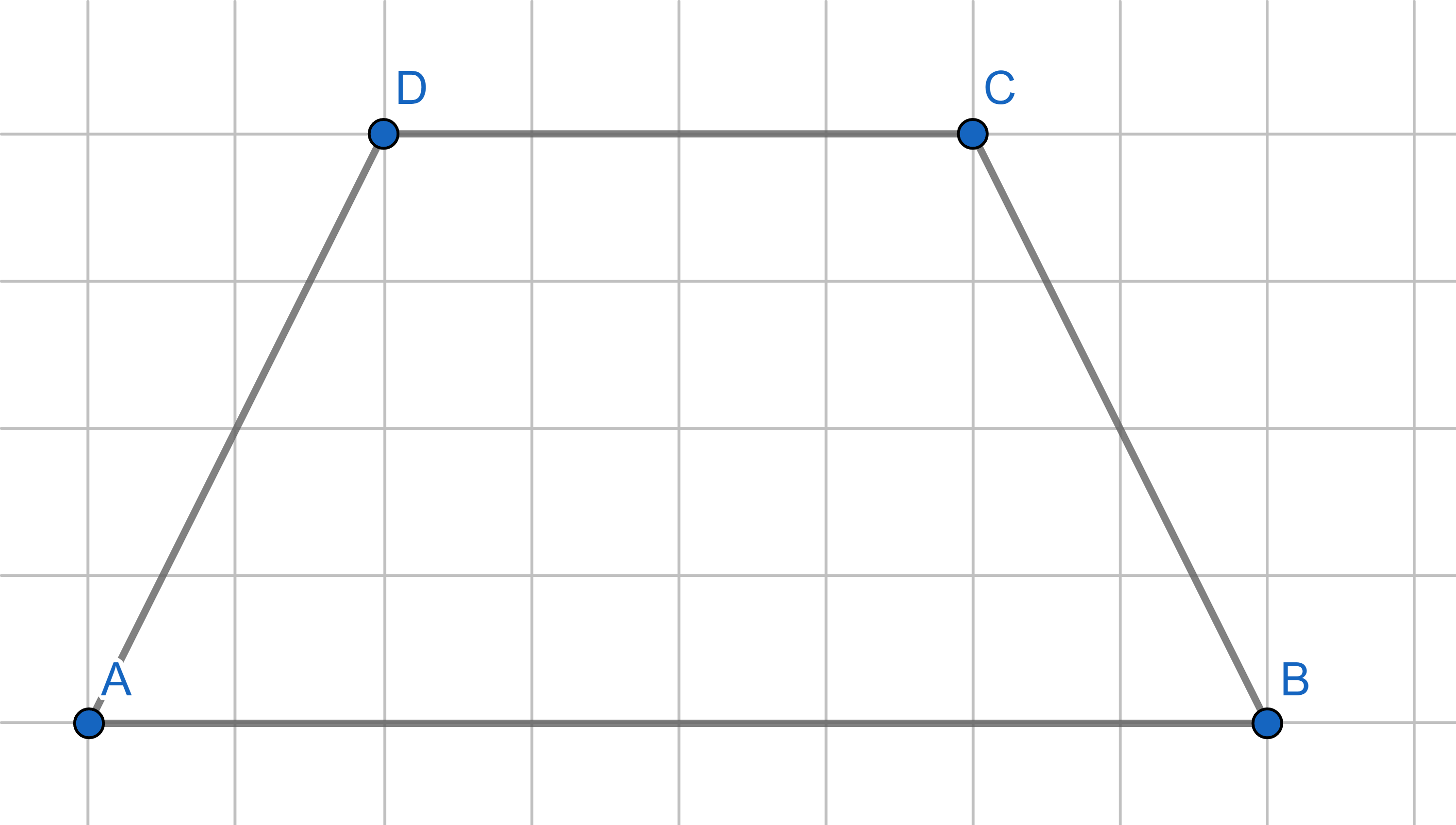
Divide the trapezium into two parts such that they can be reassembled to make a triangle.
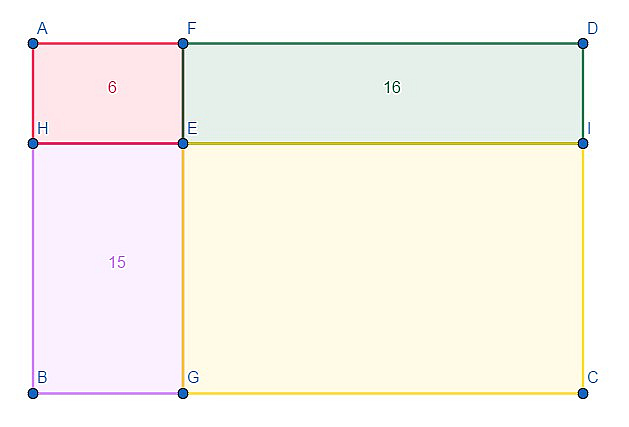
In a square \(ABHI\) two smaller squares are drawn: \(ACFG\) with area \(16\) and \(BCED\) with area \(4\). Find the area of hexagon \(DEFGIH\).