Problems
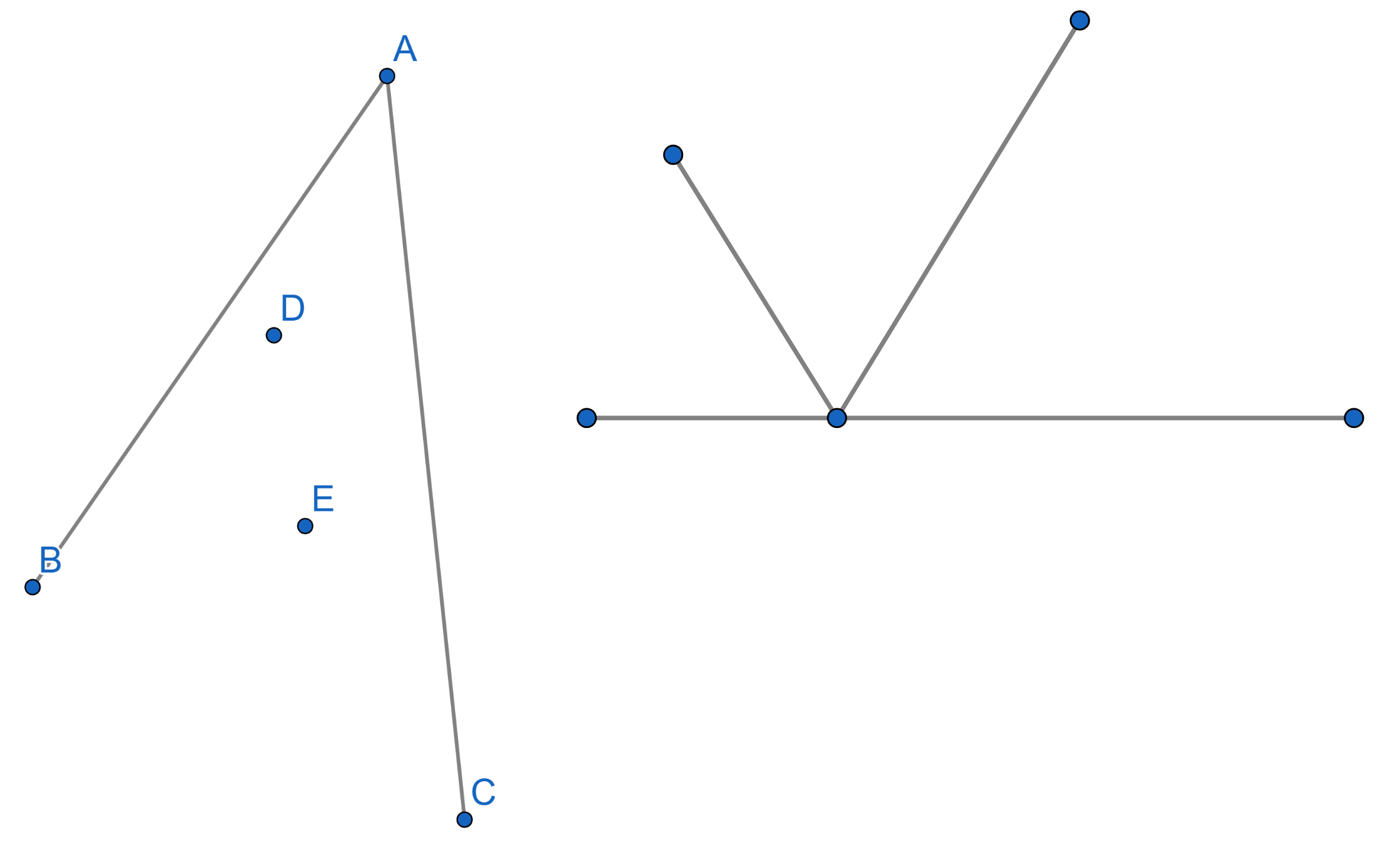
Between two mirrors \(AB\) and \(AC\), forming a sharp angle two points
\(D\) and \(E\) are located. In what direction should
one shine a ray of light from the point \(D\) in such a way that it would reflect off
both mirrors and hit the point \(E\)?
If a ray of light comes towards a surface under a certain angle, it is
reflected with the same angle as on the picture.
Consider a set of natural numbers \(A\), consisting of all numbers divisible by \(6\), let \(B\) be the set of all natural numbers divisible by \(8\), and \(C\) be the set of all natural numbers divisible by \(12\). Describe the sets \(A\cup B\), \(A\cup B\cup C\), \(A\cap B\cap C\), \(A-(B\cap C)\).
Let \(a\), \(b\) and \(c\) be the three side lengths of a triangle. Does there exist a triangle with side lengths \(a+1\), \(b+1\) and \(c+1\)? Does it depend on what \(a\), \(b\) and \(c\) are?
There is a triangle with side lengths \(a\), \(b\)
and \(c\). Can you form a triangle with
side lengths \(\frac{a}{b}\), \(\frac{b}{c}\) and \(\frac{c}{a}\)? Does it depend on what \(a\), \(b\)
and \(c\) are? Give a proof if it is
always possible or never possible. Otherwise, construct examples to show
the dependence on \(a\), \(b\) and \(c\).
Recall that a triangle can be drawn with side lengths \(x\), \(y\)
and \(z\) if and only if \(x+y>z\), \(y+z>x\) and \(z+x>y\).
There is a triangle with side lengths \(a\), \(b\)
and \(c\). Does there exist a triangle
with side lengths \(|a-b|\), \(|b-c|\) and \(|c-a|\)? Does it depend on what \(a\), \(b\)
and \(c\) are?
Recall that a triangle can be formed with side lengths \(x\), \(y\)
and \(z\) if and only if all the
inequalities \(x+y>z\), \(y+z>x\) and \(z+x>y\) hold.
There is a triangle with side lenghts \(a\), \(b\) and \(c\). Does there exist a triangle with sides of lengths \(a^2+bc\), \(b^2+ca\) and \(c^2+ab\)? Does it depend on the values of \(a\), \(b\) and \(c\)?
Prove that the set of all finite subsets of natural numbers \(\mathbb{N}\) is countable. Then prove that the set of all subsets of natural numbers is not countable.
Today you saw two infinitely long buses with seats numbered as \(1,2,3,...\) carrying infinitely many guests each arriving at the full hotel. How do you accommodate everyone?
Now there are finitely many infinitely long buses with seats numbered as \(1,2,3,...\) carrying infinitely many guests each arriving at the full hotel. Now what do you do?
How about infinitely many very long buses with seats numbered \(1,2,3...\), each carrying infinitely many guests, all arriving at the hotel. Assume for now that the hotel is empty. But that seems like a lot of guests to accommodate. What should you do?