Problems
The gcd of numbers \(a\) and \(b\) is \(72\). What can be their smallest possible product? What could be their greatest possible product?
a) Two numbers, \(a\) and \(b\), are relatively prime and their product
is equal to \(60\). What could these
numbers be? Find all the possibilities.
b) The GCD of two numbers, \(c\) and
\(d\), is \(18\) and their product is \(2^4 \times 3^5 \times 7\). What could these
numbers be? Find all the answers.
a) Can you measure \(5\) litres of
milk using two buckets of volumes \(4\)
and \(11\) litres respectively?
b) Can you measure \(7\) litres of milk
using buckets of volumes \(8\) and
\(12\) litres respectively?
a) A mighty dragon has several rubies in his treasure. He is able to
divide the rubies into groups of \(3\),
\(5\) or \(11\). How many rubies does he have, if we
know that is fewer than \(200\)?
b) The same dragon also has some emeralds. He is \(6\) emeralds short to be able to divide
them into groups of \(13\), one emerald
short to be able to divide them into groups of \(5\), but if he wants to divide them into
groups of \(8\), he is left with one
emerald. How many emeralds does he have if we know it is fewer than
\(500\)?
Let \(n\) be a natural number. Show that the fraction \(\frac{21n+4}{14n+3}\) is irreducible, i.e. it cannot be simplified.
Let \(m\) and \(n\) be two positive integers with \(m<n\) such that \[\gcd(m,n)+ \text{lcm}(m,n)=m+n.\] Show that \(m\) divides \(n\).
The numbers \(x,a,b\) are natural. Show that \(\gcd(x^a -1,x^b-1) = x^{\gcd(a,b)}-1\).
Let \(p\) be a prime number bigger than \(3\). Prove that \(p^2-1\) is a multiple of 24.
Is it possible to draw \(K_5\) without intersecting edges on a Möbius band? Recall that \(K_5\) is the complete graph on \(5\) vertices. That is, \(5\) points with an edge between every pair of different points.
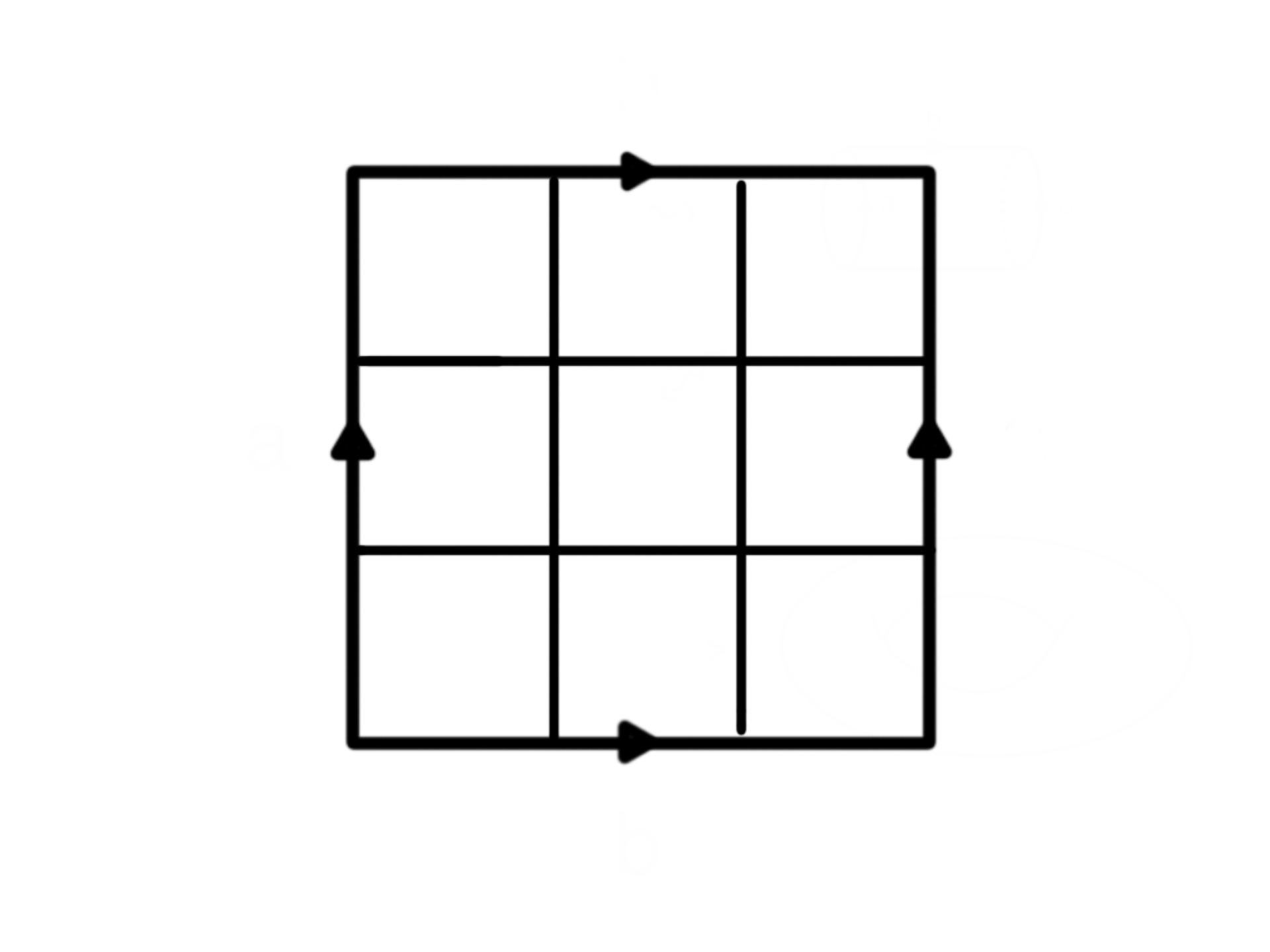
In chess, knights can move one square in one direction and two squares in a perpendicular direction. This is often seen as an ‘L’ shape on a regular chessboard. A closed knight’s tour is a path where the knight visits every square on the board exactly once, and can get to the first square from the last square.
This is a closed knight’s tour on a \(6\times6\) chessboard.
Can you draw a closed knight’s tour on a \(3\times3\) torus? That is, a \(3\times3\) square with both pairs of opposite sides identified in the same direction, like the diagram below.