Problems
Today we will solve some problems about finding areas of geometric figures. You only need to know how to calculate the area of a rectangle, a triangle and a circle to be able to solve every problem in this set. Here is a brief description of the area formula for each shape.
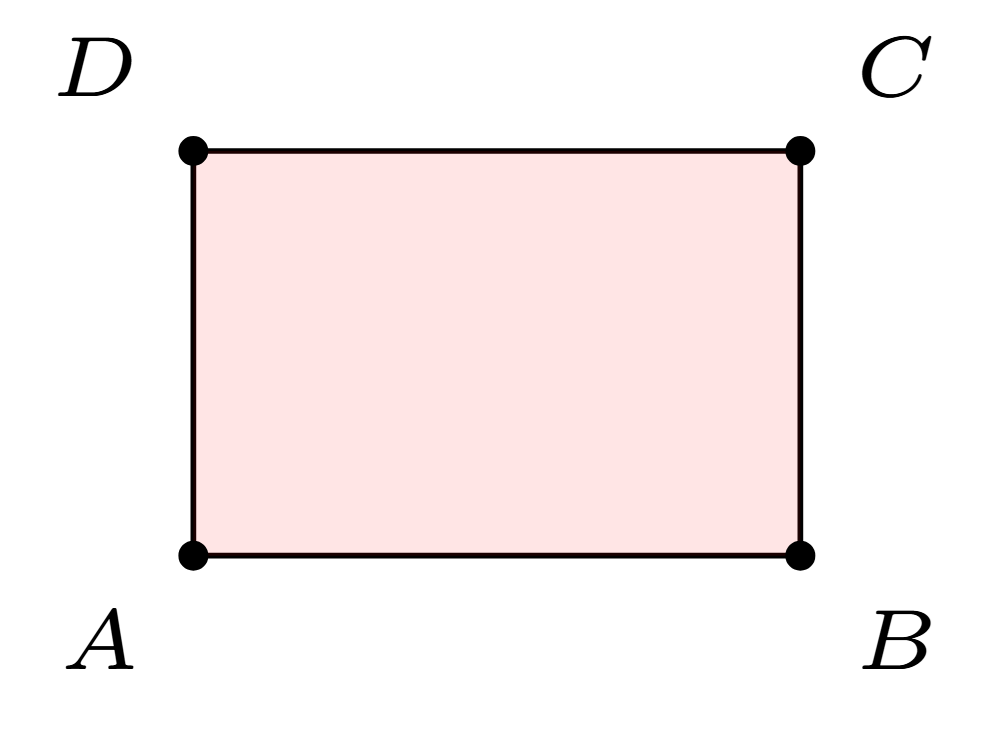
We start with rectangles because they are easy. In the picture below, one way to find the area of the rectangle is to multiple the length of the side \(AB\) by the length of the side \(AD\).
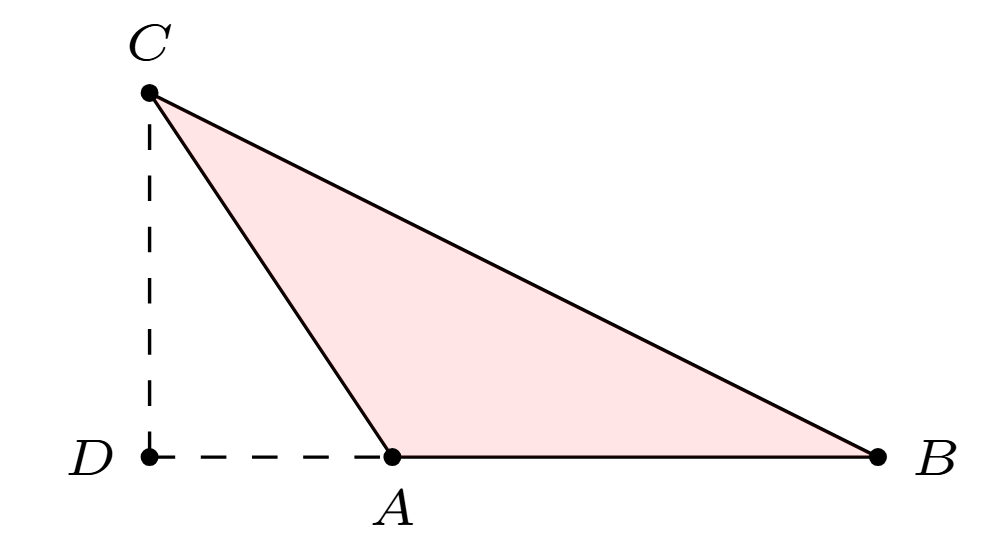
Next we consider the area of a triangle. In general, the area of a triangle is given by \(\frac{1}{2}bh\), where \(b\) is the length of a chosen base and \(h\) is the height (the length of the altitude corresponding to that base). Finding a base and a corresponding altitude is usually straightforward. However, it can be a bit tricky if the altitude lies outside the triangle. See the picture below for one such case. The segment \(AB\) is the base and \(CD\) is the altitude.
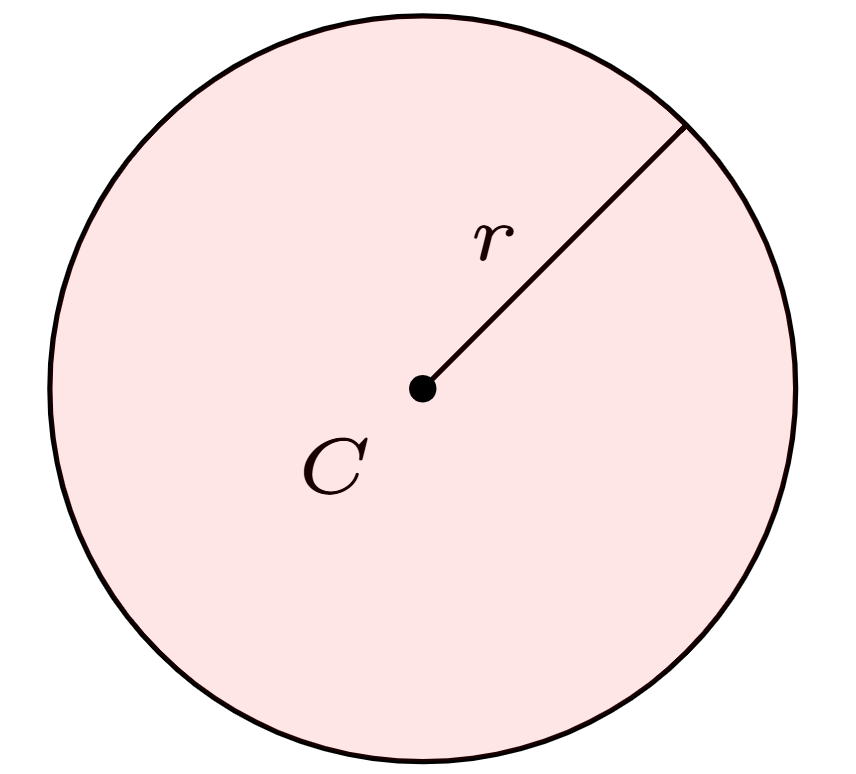
At last, we come to the area of a circle. If a circle has radius \(r\), its area is \(\pi r^2\). A fully rigorous proof requires calculus! The number \(\pi\) is approximately 3.14159 to five decimal points.
Find the mistake in the sequence of equalities: \(-1=(-1)^{\frac{2}{2}}=((-1)^2)^{\frac{1}{2}}=1^{\frac{1}{2}}=1\).
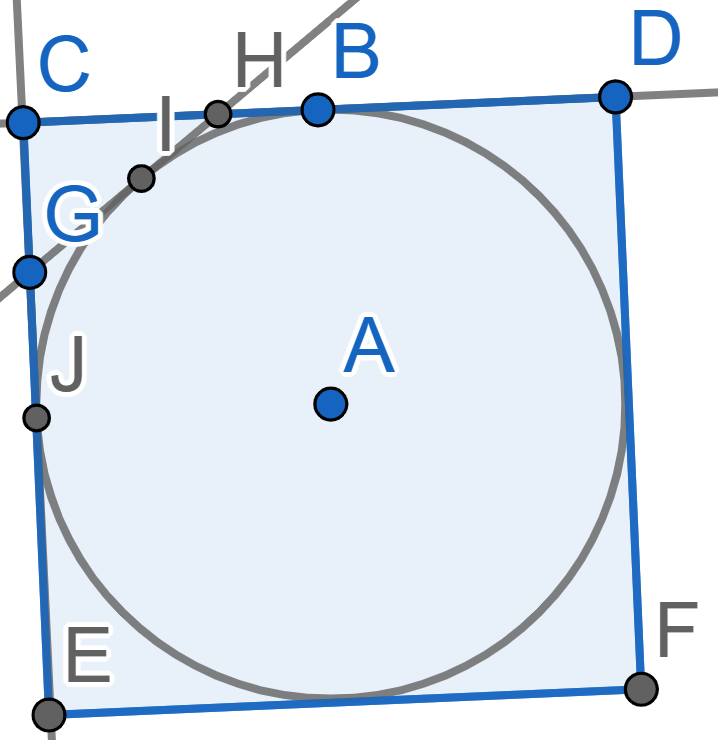
A circle with center \(A\) is inscribed into a square \(CDFE\). A line \(GH\) intersects the sides \(CD\) and \(CE\) of the square and is tangent to the circle at the point \(I\). Find the perimeter of the triangle \(CHG\) (the sum of lengths of all the sides) if the side of the square is \(10\)cm.
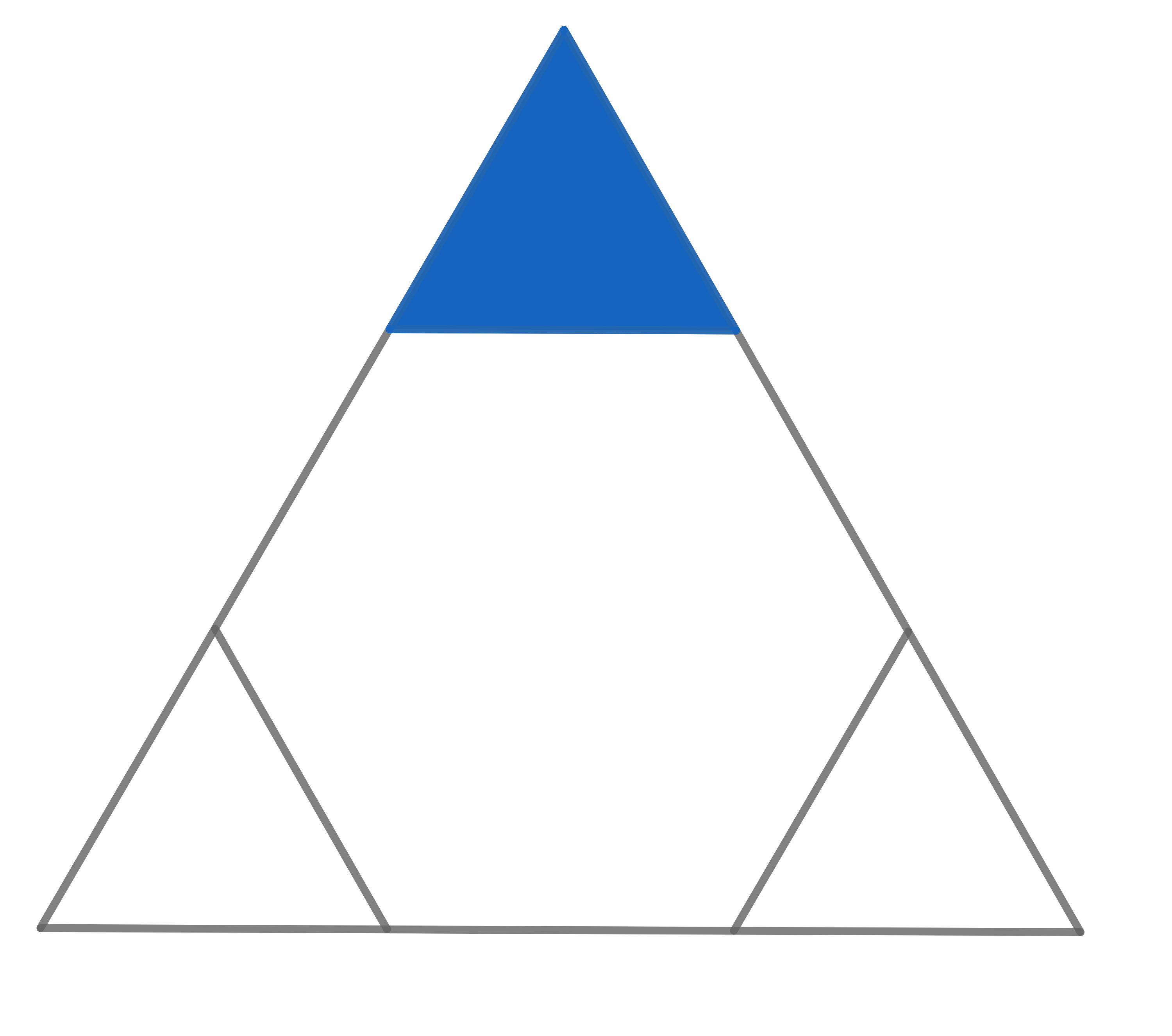
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.
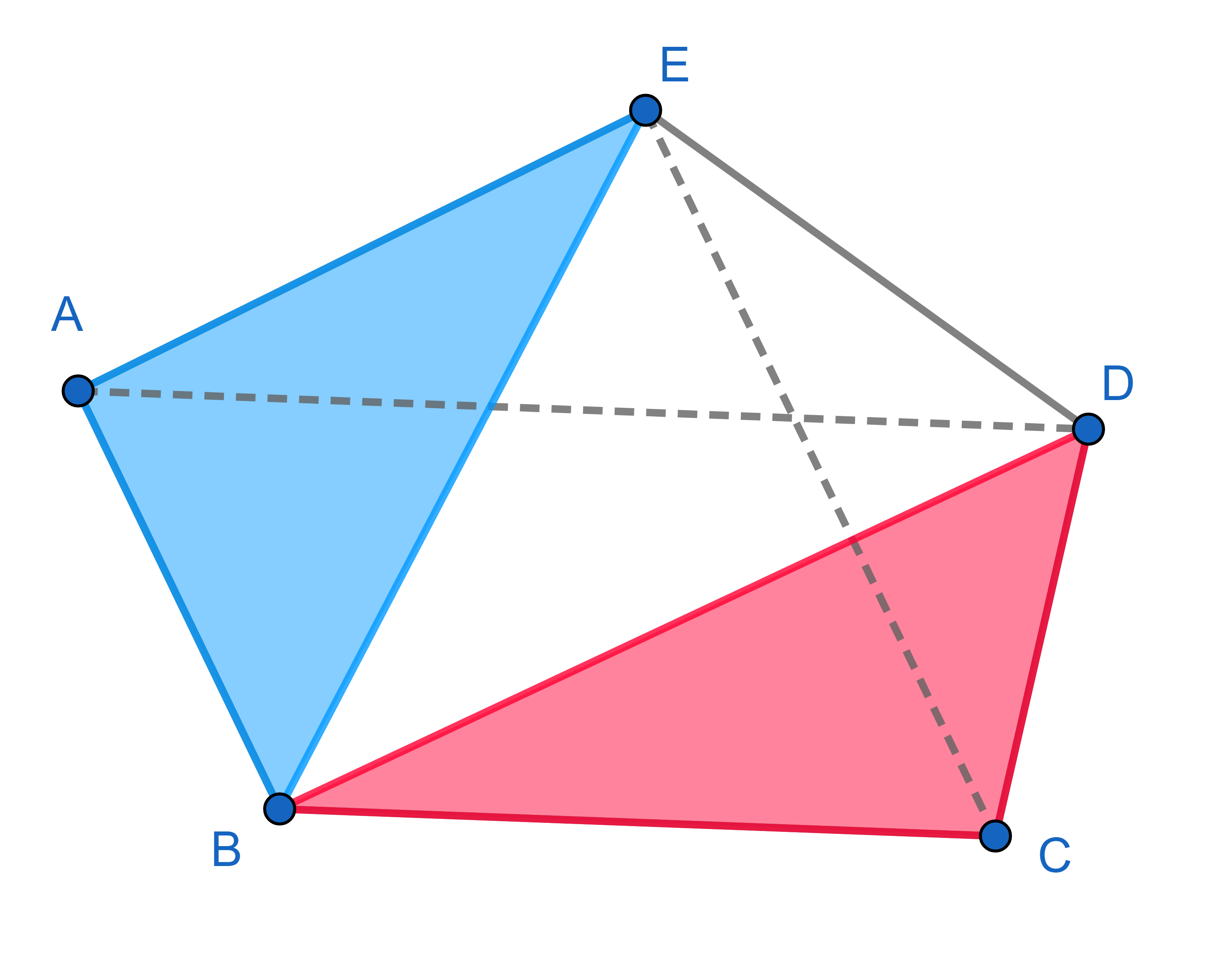
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.
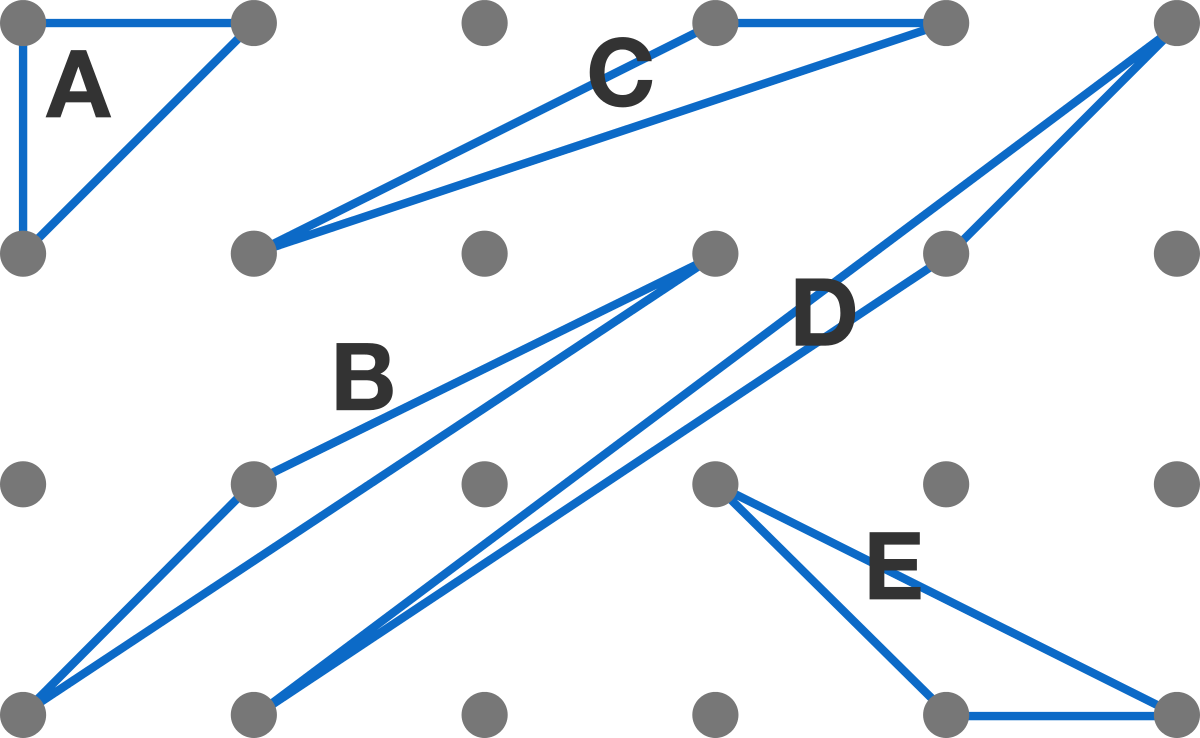
Which triangle has the largest area? The dots form a regular grid.
What is the ratio between the red and blue area? All shapes are semicircles and the red ones have equal radii.

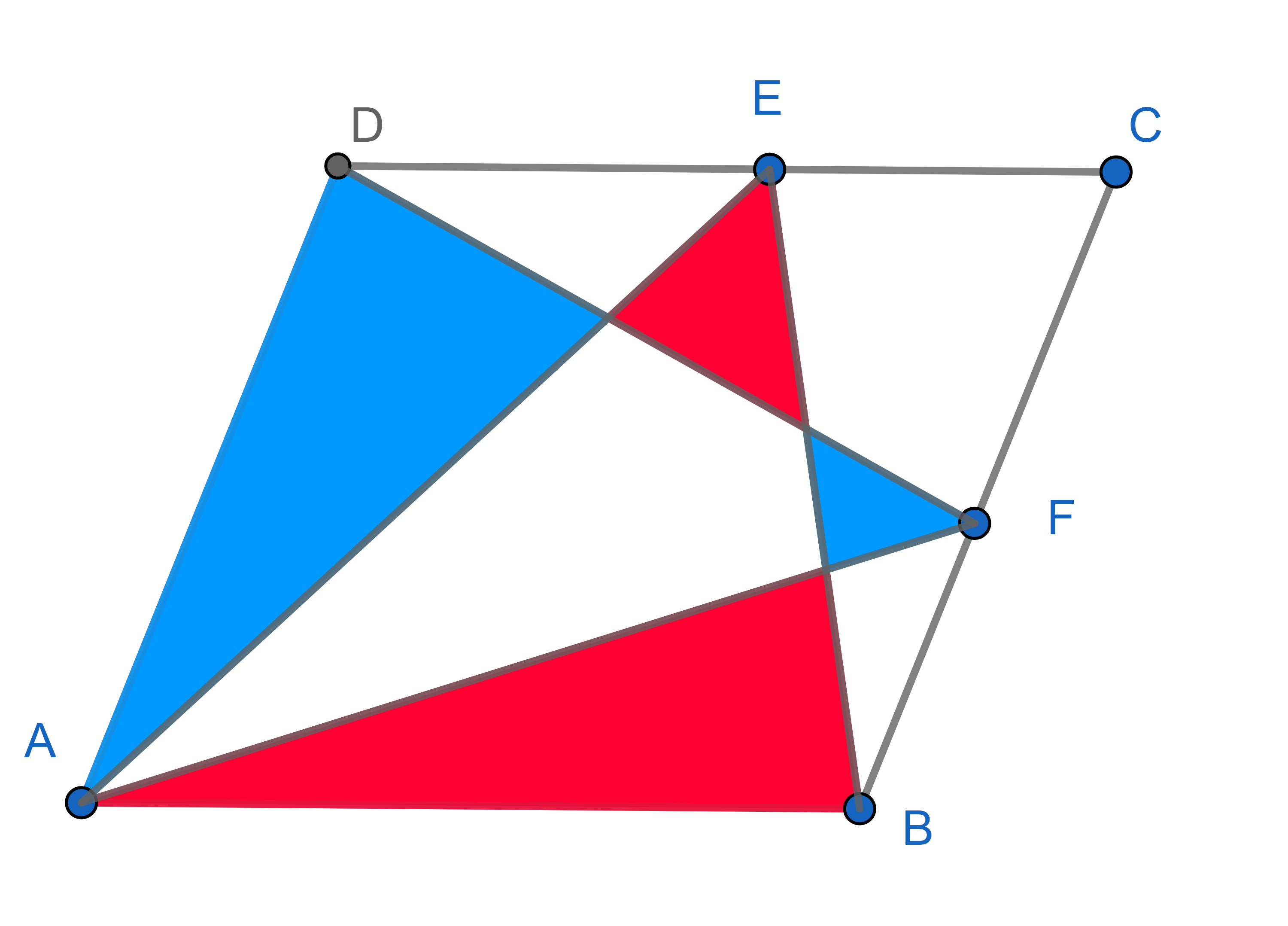
In a parallelogram \(ABCD\), point \(E\) belongs to the side \(CD\) and point \(F\) belongs to the side \(BC\). Show that the total red area is the same as the total blue area:
The figure below is a regular pentagram. What is larger, the black area or the blue area?

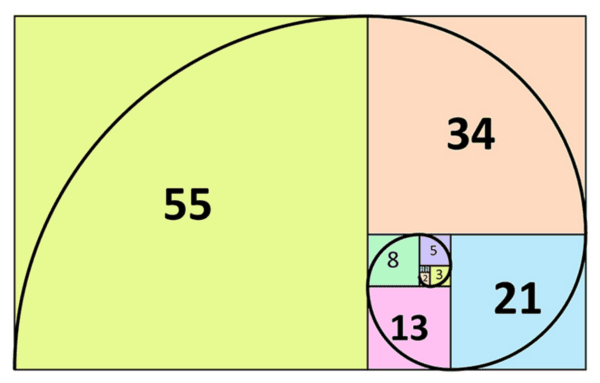
This week we’re looking at Fibonacci numbers, and other sequences of numbers.
We say that the ‘zeroth’ Fibonacci number is \(0\) and the first Fibonacci number is \(1\). Then, from that point, every Fibonacci number is found by adding the two previous Fibonacci numbers. This means that the sequence begins \(0,1,1,2,3,5,8,13,21,34,55,89,144,...\)
The Fibonacci numbers hide lots of patterns which we’ll explore today. The spiral below is formed by taking squares whose side lengths are Fibonacci numbers, and drawing quarter circles in each square.