Problems

This week we’re looking at Fibonacci numbers, and other sequences of numbers.

We say that the ‘zeroth’ Fibonacci number is \(0\) and the first Fibonacci number is \(1\). Then, from that point, every Fibonacci number is found by adding the two previous Fibonacci numbers. This means that the sequence begins \(0,1,1,2,3,5,8,13,21,34,55,89,144,...\)

The Fibonacci numbers hide lots of patterns which we’ll explore today. The spiral below is formed by taking squares whose side lengths are Fibonacci numbers, and drawing quarter circles in each square.

Prime numbers are like atoms that build every integer number. That is, a prime decomposition of a number is unique and then we can use it to find the number’s factors. Today we will explore this idea a bit more.

We will introduce a couple of new terms. First, a common divisor of two numbers is simply a number that both of these numbers can be divided by. Two numbers which have no common divisors (except from 1) are called relatively prime. We can establish if two numbers are relatively prime by looking at their prime factorizations - if they share no common primes, then they cannot share a common divisor!

Out of all the common divisors two numbers have, one must be the largest. This is an important number and is called the Greatest Common Divisor (GCD). You can find it by looking at the prime factorizations of the two numbers. For every prime number appearing in both factorizations, we take the smaller power. Then we multiply all our choices together. If we divide both numbers by their GCD, the resulting numbers will have no common divisors left and so will be relatively prime.

Similar to the notion of a common divisor is the one of common multiple. It is simply a number that is divisible by both numbers. Among the common multiples, one must be the smallest – this is called the Least Common Multiple (LCM). Again, the LCM can be found by looking at the prime factorizations of the two numbers. For every prime number appearing in any of the two factorizations, we take the larger power. Then we multiply all our choices together.

Today we will be looking at tilings. We define a plane tiling as a covering of the entire plane, without any gaps or overlaps, using identical geometric shapes that can be rotated and symmetrical to each other. Usually, it is sufficient to cover a small portion of the plane with a particular pattern that can be extended to cover the entire plane.

We will also look at some tilings of finite shapes, normally rectangles. You can imagine this as tiling a floor. With a huge number of \(1\times2\) tiles, we can investigate how to tile a floor in a rectangular room if no tile can overlap the other. It’s easy to tile the floor in a \(6\times8\) room.

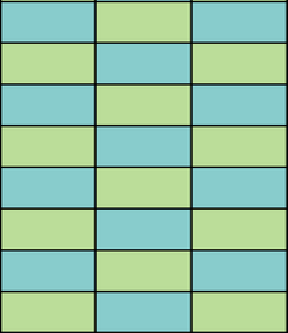
We can notice that if the floor in a room of size \(p\times q\) is tiled with \(1\times2\) tiles, then \(pq\) is even (can you explain why?). The reverse is also true; i.e. if \(pq\) is even, then the floor can be tiled with \(1\times2\) tiles in a similar way to the picture above.

However, this tiling can be cut from one side to another by a grid line without splitting any tiles. Such constructions are impractical, and this type of floor can easily become uneven. That’s why in practise irreducible tilings are used.

A tiling of a rectangle by small identical rectangles (tiles) is called irreducible if any straight cut from one side of the big rectangle to another goes across at least one of the tiles.

Among the first \(20\) Fibonacci numbers: \(F_0 = 0,F_1 = 1,F_2 = 1, F_3 = 2, F_4 = 3,..., F_{20} = 6765\) find all numbers whose digit-sum is equal to their index. For example, \(F_1=1\) fits the description, but \(F_{20} = 6765\) does not, since \(6+7+6+5 \neq 20\).

Among the first \(20\) Fibonacci numbers: \(F_0 = 0,F_1 = 1,F_2 = 1, F_3 = 2, F_4 = 3,..., F_{20} = 6765\) check whether the numbers with prime index are prime. The index is another name for a number’s place in the sequence.

Consider Pascal’s triangle: it starts with \(1\), then each entry in the triangle is the sum of the two numbers above it. Prove that the diagonals of Pascal’s triangle add up to Fibonacci numbers.

Prove for any integers \(m,n\ge0\) that \(F_{m+n} = F_{m-1}F_n + F_mF_{n+1}\).
Corollary: if \(k\mid n\), then \(F_k\mid F_n\). This can be proven by induction if we write \(n=sk\) for a natural \(s\), then \[F_{k+(s-1)k} = F_{k-1}F_{(s-1)k} + F_kF_{(s-1)k+1}.\]

Denote by \(\gcd(m,n)\) the greatest common divisor of numbers \(m,n\), namely the largest possible \(d\) which divides both \(n\) and \(m\). Prove for any \(m,n\) that \[\gcd(F_n,F_m) = F_{\gcd(m,n)}.\]

Suppose that \(p\) is a prime number. How many numbers are there less than \(p^2\) that are relatively prime to \(p^2\)?

How many cuboids are contained in an \(n\times n\times n\) cube? For example, we’ve got \(n^3\) cuboids of size \(1\times1\times1\), and obviously just \(1\) of size \(n\times n\times n\) (which is the whole cube itself). But we also have to count how many there of size \(1\times1\times2\), \(1\times2\times3\), and several more.