Problems
Simplify \(F_0-F_1+F_2-F_3+...-F_{2n-1}+F_{2n}\), where \(n\) is a positive integer.
Let us define XOR (or addition mod 2). XOR is defined for 0 and 1 only. Here is a table recording the values of XOR:
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Now we define the important concept of nim-sum. Given two natural numbers \(x\) and \(y\), we first convert them into binary representations and then compute XOR on individual digits. The resulting number, denoted \(x \oplus y\), is the nim-sum of \(x\) and \(y\). Here is an example.
| 1 | 0 | 1 | 1 | 0 | |
| XOR | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
This is simply saying \(22 \oplus 5 = 19\). Note that \(22=(10110)_2\) and \(5=(00101)_2\).
Verify \((x \oplus y) \oplus z = x \oplus (y \oplus z)\), so we can speak of \(x \oplus y \oplus z\) with no ambiguity.
Show that \(x \oplus y = 0\) if and only if \(x = y\). Remember that \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).
Show that \(\text{Nim}(x,y,z)\) is a losing position if and only if \(x \oplus y \oplus z = 0\). Remember that \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).
Is \(\text{Nim}(7,11,15)\) a winning position or a losing position? If it is a winning position, what is the optimal move?
Show that \(\text{Nim}(x_1,\dots,x_k)\) is an losing position if and only if \(x_1 \oplus \dots \oplus x_k = 0\). \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).
Imagine the Earth is a perfectly round solid ball. Let us drill from the North Pole, London and Beijing simultaneously and meet at the centre of Earth. A ball with three openings is formed. The surface of this ball is shown on the left of the picture below. Describe how to stretch this surface so that it looks like the surface of a donut with two holes as shown on the right.
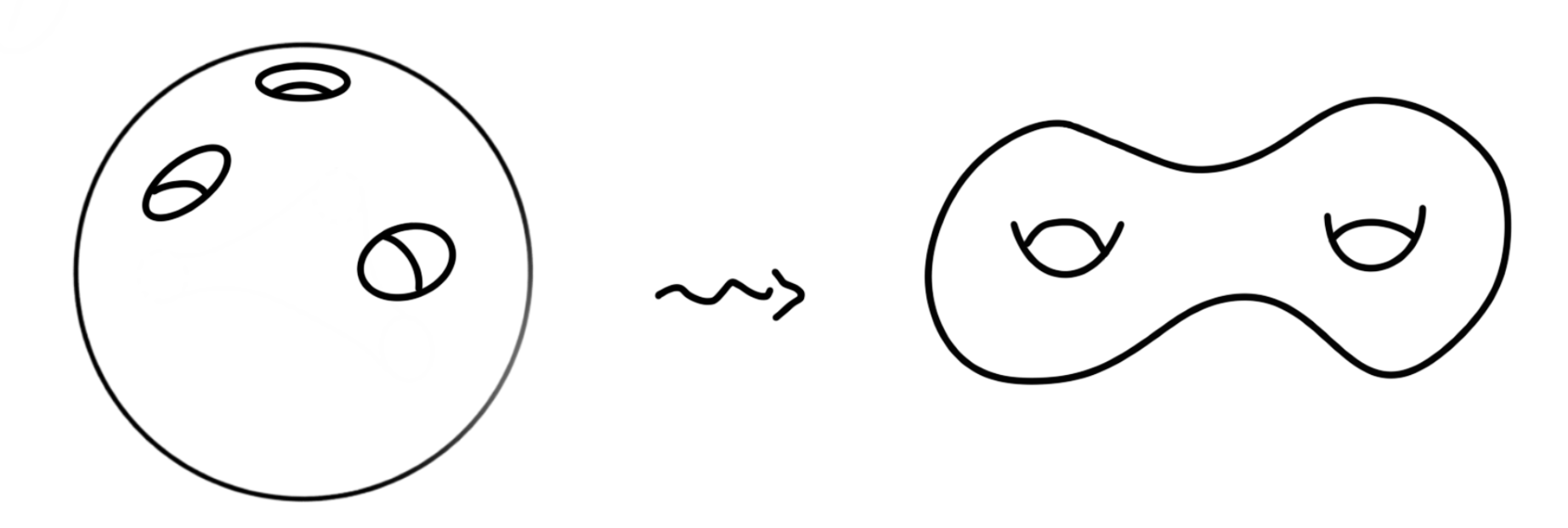
Show that there are no rational numbers \(a,b\) such that \(a^2 + b^2 = 3\).
There are infinitely many couples at a party. Each pair is separated to form two queues of people, where each person is standing next to their partner. Suppose the queue on the left has the property that every nonempty collection of people has a person (from the collection) standing in front of everyone else from that collection. A jester comes into the room and joins the right queue at the back after the two queues are formed.
Each person in the right queue would like to shake hand with a person in the left queue. However, no two of them would like to shake hand with the same person in the left queue. If \(p\) is standing behind \(q\) in the right queue, \(p\) will only shake hand with someone standing behind \(q\)’s handshake partner. Show that it is impossible to shake hands without leaving out someone from the left queue.
Suppose \(x,y\) are real numbers such that \(x < y + \varepsilon\) for every \(\varepsilon > 0\). Show that \(x \leq y\).