Problems
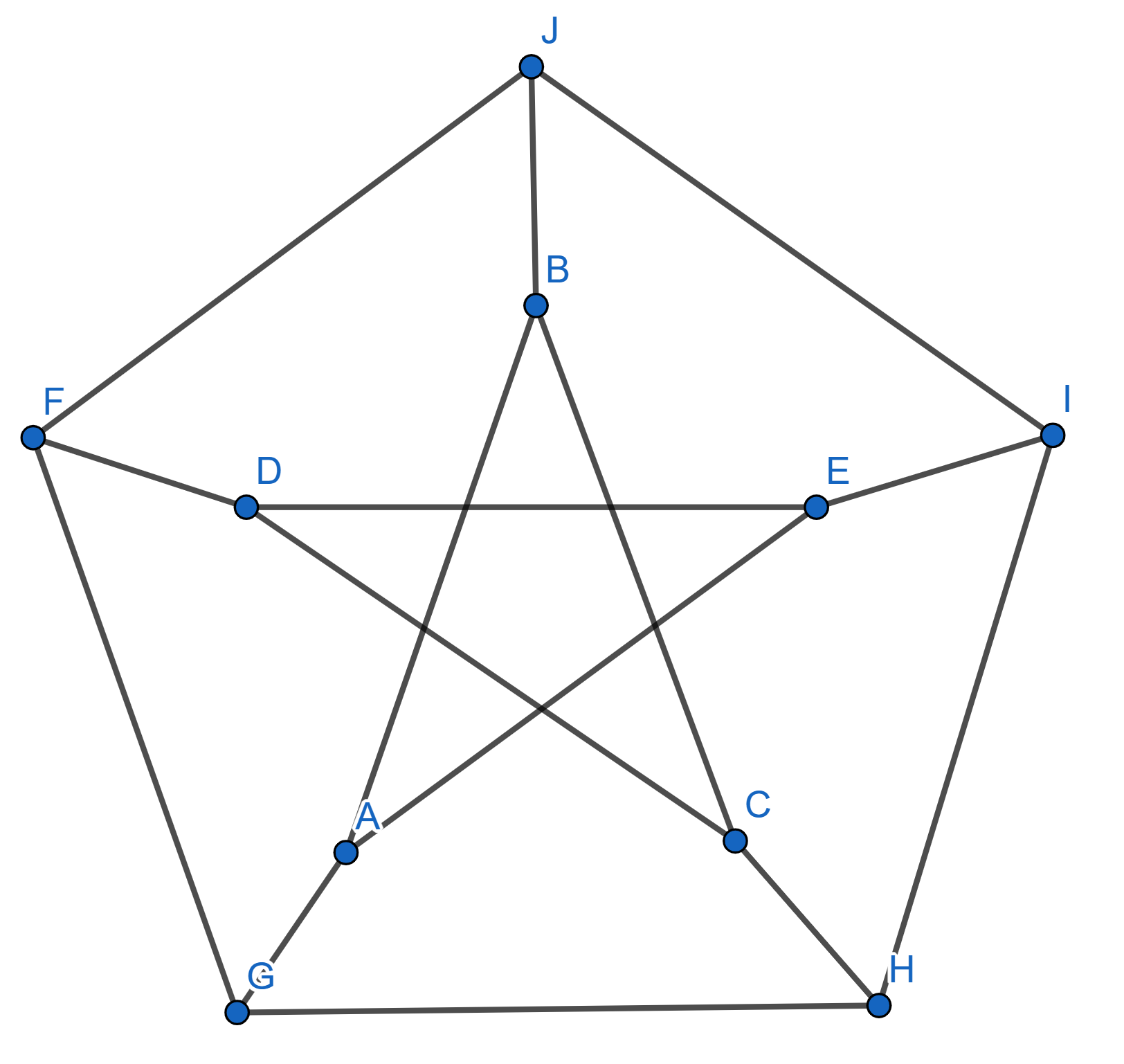
Find the minimum number of colours Raphael needs to paint the following figure in such a way that no connected points are of the same colour.
On the green and red coloured plane, show that there is always a rectangle whose vertices all have the same colour.
Hokusai uses \(7\) colours to colour the entire plane. Show that there is a way to colour the entire plane so that any two points with distance \(1\) between them must have different colours.
Tracey wants each straight line on the plane to only consist of points of two or fewer colours. What is the maximum number of colours she can use to colour the plane?
Georgia decided to only colour grid points - points where lines meet on a sheet of square grid paper. She used red and blue crayons, each at least once. The distance between adjacent grid points is \(1\). Show that there is always a segment of length \(5\) whose ends are different colours.
Banksy used three colours to colour the entire plane: red, green and
gold. Show that there are two points, distance one apart, which are the
same colour.
The same is true if he used \(4\)
colours, including grey for example, but that is significantly more
difficult to show.
This is part of a more general problem of colouring the entire plane with some number of colours and trying to avoid segments of length \(1\) with both ends of the same colour. The question is, how many colours do we need? We know \(7\) is enough and that \(3\) is not enough. The general problem is known as Hadwiger–Nelson problem and was first formulated in 1950, with those bounds found almost immediately. The next piece of progress was only made in 2018, when Aubrey de Grey found a geometrical figure with \(1581\) points (we used only \(7\) in the above proof) that shows it is not possible to only use \(4\) colours. That was later refined to \(510\) points. The general answer of whether it is \(5\), \(6\) or \(7\) colours is still unknown.
Vincent would like to colour the entire \(3\)-dimensional space in such a way that no two points distance \(1\) apart are of the same colour. Prove that he needs at least \(5\) colours.
Just like atoms are the building blocks of molecules, prime numbers are the building blocks of integers, or whole numbers. What do we mean by this?
Well, every molecule is composed of atoms, and each atom is an atom of a particular element, like carbon or nitrogen. Similarly, every positive integer (except \(1\)) can be broken down into prime numbers. We can say this formally as follows:
The Fundamental Theorem of Arithmetic says that any natural number greater than \(1\) can be uniquely expressed as a product of prime numbers in non-decreasing order. For example: \[630=2\times3\times3\times5\times7=2\times3^2\times5\times7.\]
Recall that a number is composite if it is a product of two smaller, natural numbers. For example, \(6 = 2\times3\). Otherwise, and if the number is not equal to \(1\), it is called prime. The number \(1\) is neither prime nor composite.
Modulo operation: We look at division. For example \(41=2\times15+11\) is the division of \(41\) (the dividend) by \(15\) (the divisor) with remainder
\(11\), and \(5=0\times7+5\) is the division of \(5\) by \(7\) with the remainder \(5\). More generally, when we divide \(a\) by \(b\), we’re looking for non-negative
integers \(c\) and \(d\) (\(d<b\)) such that \(a=c\times b+d\).
In the case of \(45\) divided by \(15\), we get \(3\) with remainder \(0\) - in which case we say “\(15\) divides \(45\)", or “\(45\) is divisible by \(15\)". We can write this as \(15|45\).
We can deduce from the Fundamental Theorem of Arithmetic that if a product of two natural numbers is divisible by a prime number, then one of these numbers is divisible by this prime number. For example, \(7|7007=13\times539\) tells us that \(7\) divides \(13\) or \(539\). Clearly \(7\nmid13\), so we know \(7|539\).
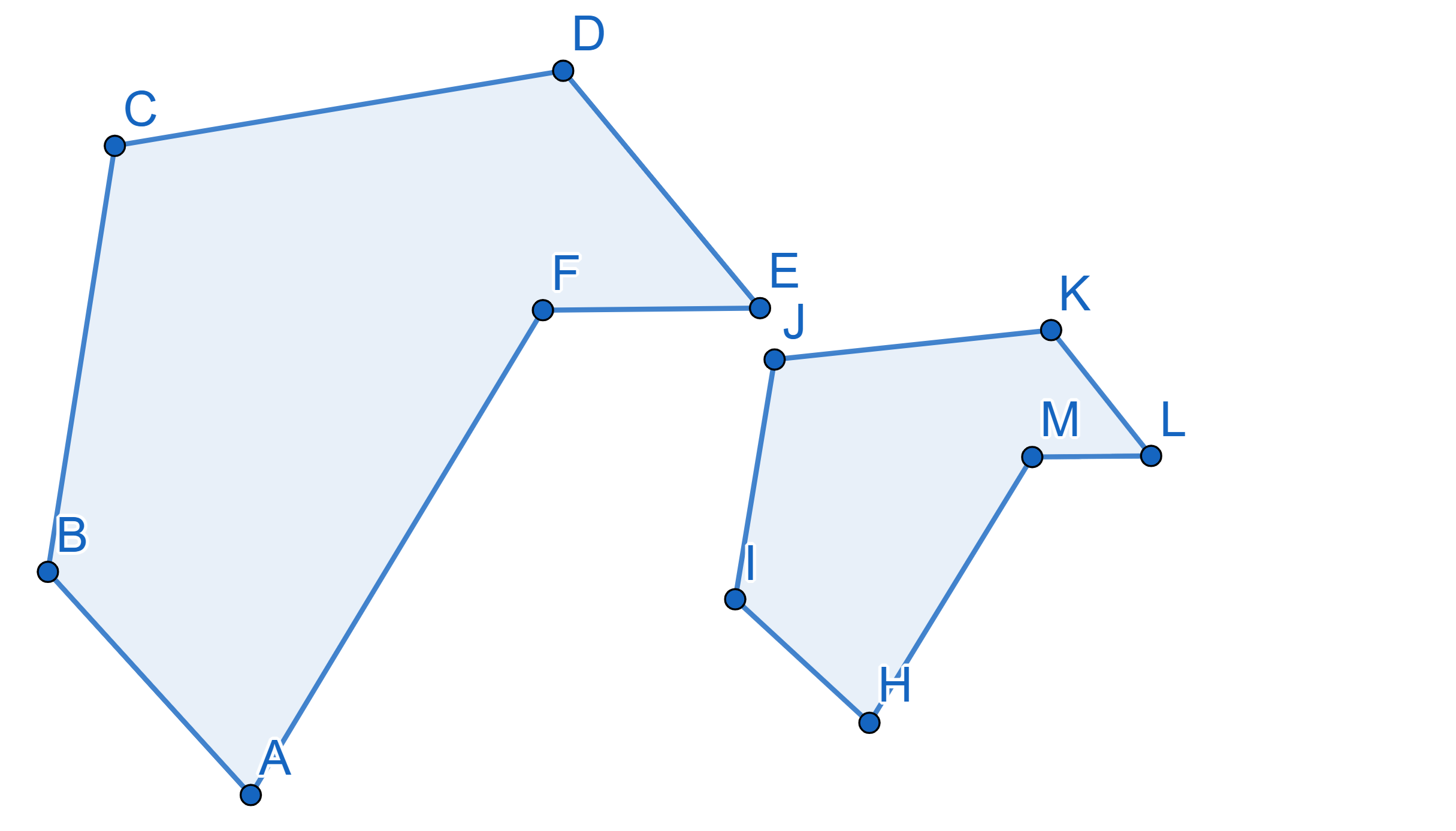
It is often the case in geometric situations that figures look very
similar, but not quite equal. Two polygons on the plane are called
similar if and only if ALL their corresponding angles
are equal AND the ratio between ALL
the corresponding sides is the same.
The relation between the corresponding sides, in our case it’s \(\frac{|AB|}{|IH|}\), is called the
similarity coefficient between the figures. It is common practice to
write vertices of similar figures in the order that respects the
similarity.
We will find some criteria for determining similarity and apply them to solve problems. The statements of some examples and problems may be helpful for problems coming after them!
Let \(\triangle ABC\) and \(\triangle DEF\) be triangles such that the following angles are equal: \(\angle ABC = \angle DEF\) and \(\angle ACB = \angle DFE\). Prove that \(\triangle ABC\) and \(\triangle DEF\) are similar triangles.