Problems
The medians \(AD\) and \(BE\) of the triangle \(\triangle ABC\) intersect at the point \(F\). Prove that \(\triangle AFB\) and \(\triangle DFE\) are similar. What is their similarity coefficient?
In a triangle \(\triangle ABC\), the angle \(\angle B = 90^{\circ}\) . The altitude from point \(B\) intersects \(AC\) at \(D\). We know the lengths \(|AD|=9\) and \(|CD|=25\). What is the length \(|BD|\)?
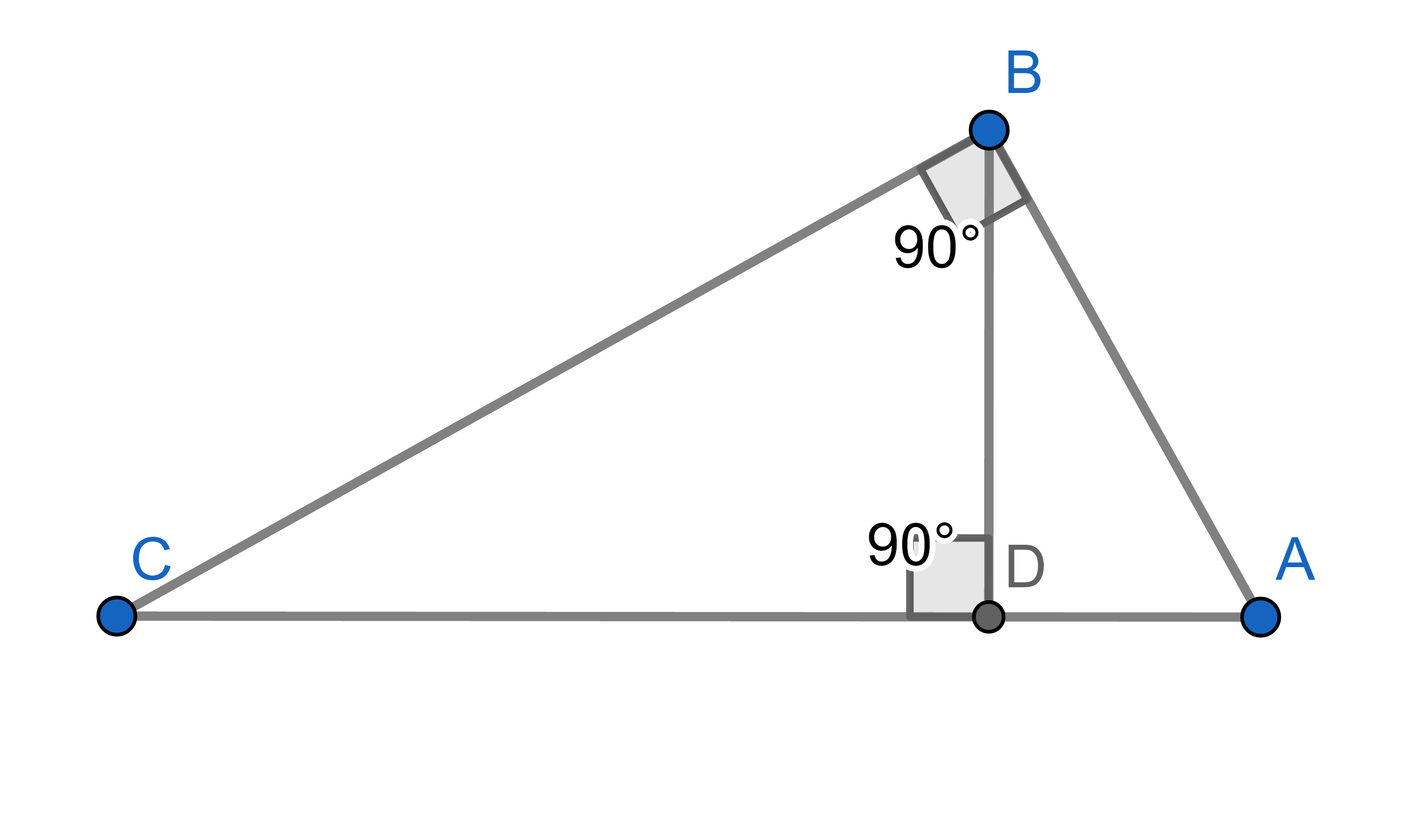
Let \(\triangle ABC\) and \(\triangle DEF\) be two triangles such that \(\angle ACB = \angle DFE\) and \(\frac{|DF|}{|AC|} = \frac{|EF|}{|BC|}\). Prove that \(\triangle ABC\) and \(\triangle DEF\) are similar.
Let \(AA_1\) and \(BB_1\) be the medians of the triangle \(\triangle ABC\). Prove that \(\triangle A_1B_1C\) and \(\triangle BAC\) are similar. What is the similarity coefficient?
Let \(AD\) and \(BE\) be the heights of the triangle \(\triangle ABC\), which intersect at the point \(F\). Prove that \(\triangle AFE\) and \(\triangle BFD\) are similar.
Let \(AD\) and \(BE\) be the heights of the triangle \(\triangle ABC\). Prove that \(\triangle DEC\) and \(\triangle ABC\) are similar.
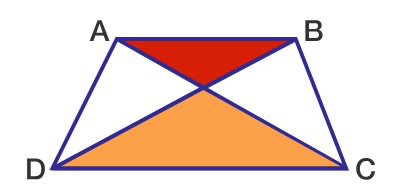
The area of the red triangle is \(25\) and the area of the orange triangle is \(49\). What is the area of the trapezium \(ABCD\)?
Prove that the ratio of perimeters of similar polygons is equal to the similarity coefficient.
Let \(CB\) and \(CD\) be tangents to the circle with the centre \(A\), let \(E\) be the point of intersection of the line \(AC\) with the circle. Draw \(FG\) as the segment of a tangent drawn through the point \(E\) between the lines \(CB\) and \(CD\). Find the length \(|FG|\) if the radius of the circle is \(15\) and \(|AC| = 39\).
Prove that the relation between areas of two similar polygons equals to the square of their similarity coefficient.