Problems

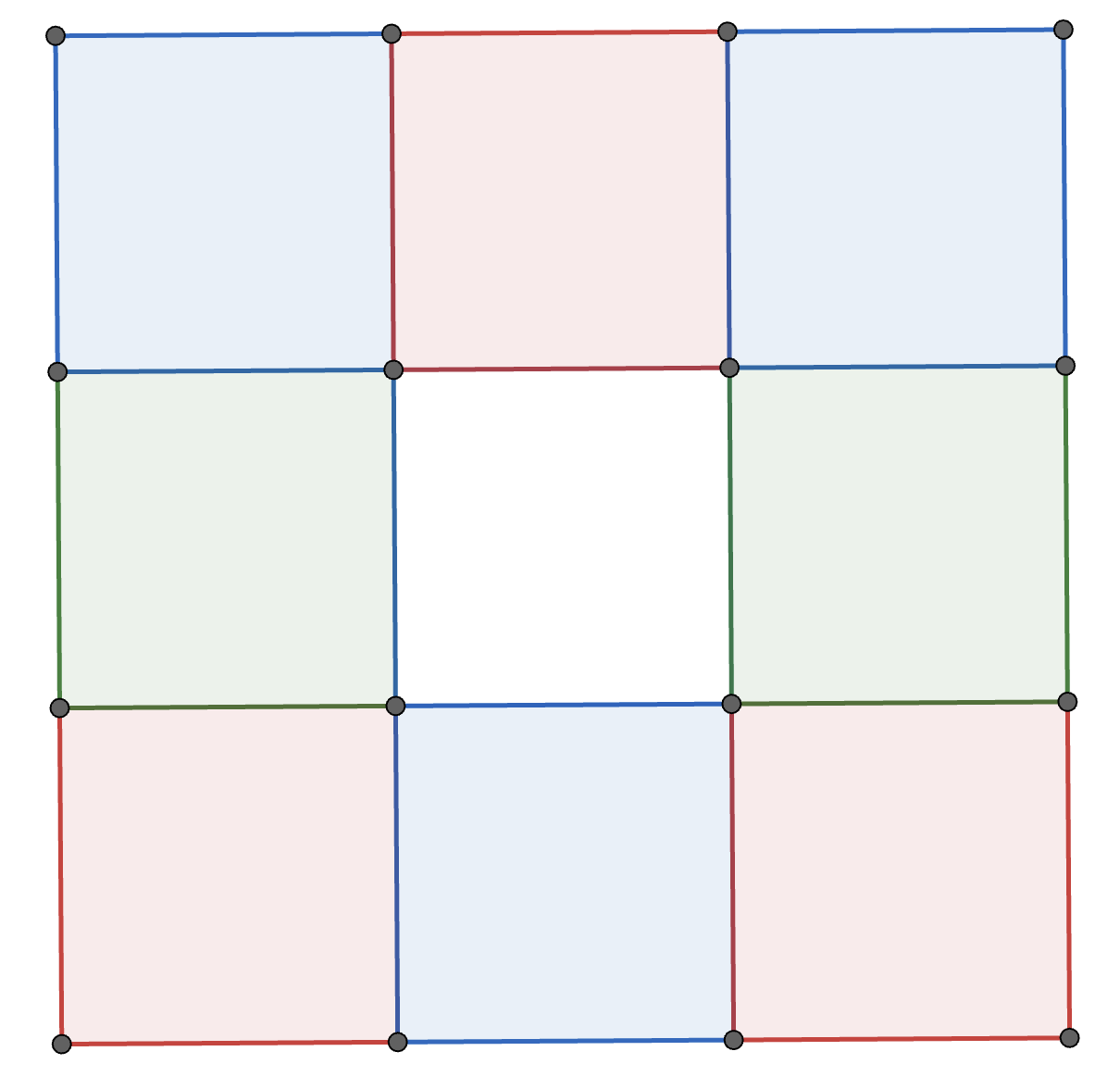
Each square in a \(3\times3\) grid of squares is coloured red, white, blue, or green so that every \(2\times2\) square contains one square of each color. One such colouring is shown below. How many different colourings are possible?

For any positive integer \(k\), the factorial \(k!\) is defined as a product of all integers between 1 and \(k\) inclusive: \(k! = k \times (k-1) \times ... \times 1\). What’s the remainder when \(2025!+2024!+2023!+...+3!+2!+1!\) is divided by \(8\)?

Find all functions \(f\) from the real numbers to the real numbers such that \(xy=f(x)f(y)-f(x+y)\) for all real numbers x and y.

There are two imposters and seven crewmates on the rocket ‘Plus’. How many ways are there for the nine people to split into three groups of three, such that each group has at least two crewmates? The two imposters and seven crewmates are all distinguishable from each other, but we’re not concerned with the order of the three groups.

For example: \(\{I_1,C_1,C_2\}\), \(\{I_2,C_3,C_4\}\) and \(\{C_5,C_6,C_7\}\) is the same as \(\{C_3,C_4,I_2\}\), \(\{C_5,C_6,C_7\}\) and \(\{I_1,C_2,C_1\}\) but different from \(\{I_2,C_1,C_2\}\), \(\{I_1,C_3,C_4\}\) and \(\{C_5,C_6,C_7\}\).

Let \(n\) be a natural number, and let \(d(n)\) be the number of factors of \(n\). For example, the factors of \(6\) are \(1,2,3,6\), so \(d(6)=4\). Find all \(n\) such that \(d(n)+d(n+1)=5\).

Draw the plane tiling with regular hexagons.

Let \(\sigma(n)\) be the sum of the divisors of \(n\). For example, \(\sigma(12)=1+2+3+4+6+12=28\). We use \(\gamma\) to denote the Euler-Mascheroni constant - one way to define this is as \(\gamma:=\lim_{n\to\infty}(\sum_{k=1}^n\frac{1}{n}-\log n)\).

Prove that \(\sigma(n)<e^{\gamma}n\log\log n\) for all integers \(n>5040\).

Let \(n\) be an integer bigger than \(1\), and \(p\) a prime number. Suppose that \(n\) divides \(p-1\) and \(p\) divides \(n^3-1\). Prove that \(4p-3\) is a square number.

Let \(n\) be a composite number. Arrange the factors of \(n\) greater than \(1\) in a circle. When can this be done such that neighbours in the circle are never coprime?

Let \(x\), \(y\), \(z\) and \(w\) be non-negative integers. Find all solutions to \(2^x3^y-5^z7^w=1\).