Problems

A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.

Show that \(|BE|=|DE|\).

Are there any two-digit numbers which are the product of their digits?

How many \(10\)-digit numbers are there such that the sum of their digits is \(3\)?

The sum of digits of a positive integer \(n\) is the same as the number of digits of \(n\). What are the possible products of the digits of \(n\)?

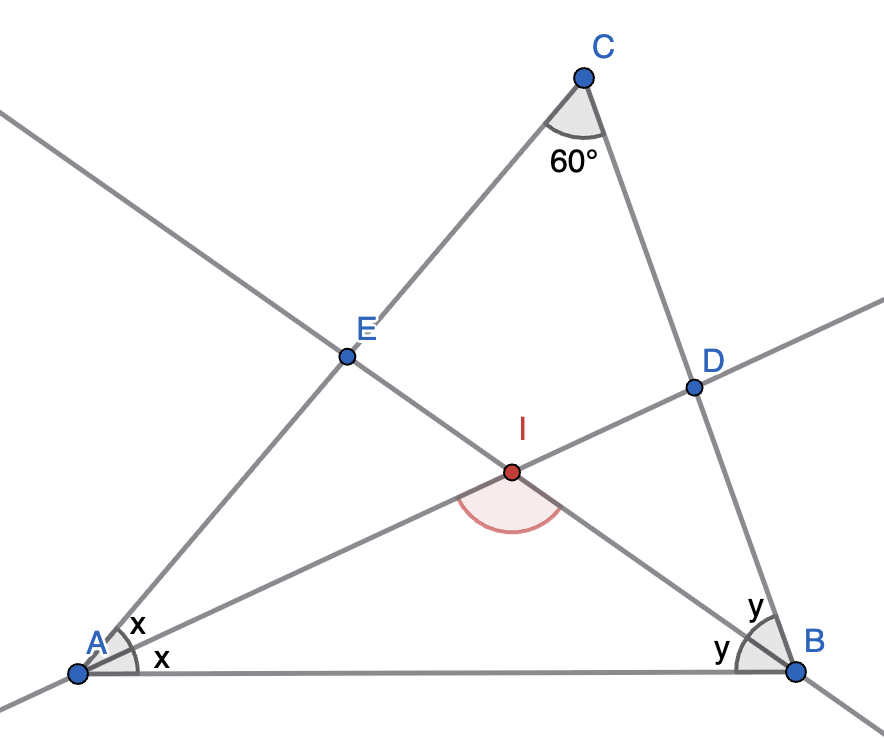
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).

Find the angle \(\angle AIB\), marked in red.

Find, with proof, all integer solutions of \(a^3+b^3=9\).