Problems

Consider a graph with four vertices and where each vertex is connected to every other one (this is called the complete graph of four vertices, sometimes written as \(K_4\)). We write the numbers \(10,20,30,\) and \(40\) on the vertices. We play the following game: choose any vertex, and subtract three from that vertex, and add one to each of the three other vertices, so an example could be:

After playing this game for some number of steps, can we make the graph have the number \(25\) on each vertex?

Every year the citizens of the planet “Lotsofteeth" enter a contest to see who has the most teeth.
This year the judge notices:

1. Nobody has 0 teeth (everyone has at least 1).

2. There are more people in the contest than the most teeth that any one person has. (For example, if the most teeth anyone has is 27, then there are more than 27 people participating in the contest.)

Must there be two people who have exactly the same number of teeth? Explain why.

Fred and George had two square cakes. Each made two straight cuts on his cake from edge to edge. However, one ended up with three pieces, and the other with four. How could this be?

Remember that two shapes are congruent if they are the same in shape and size, even if one is flipped or turned around. For example, here are two congruent shapes:

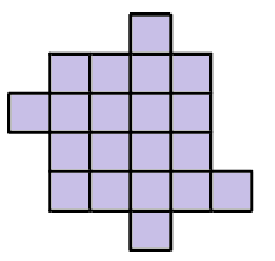
Cut the following shape into four congruent figures:

A cube net is a 2D shape that can be folded into a cube. For example, in the following diagram we show a cube net and the steps that fold it into a cube:

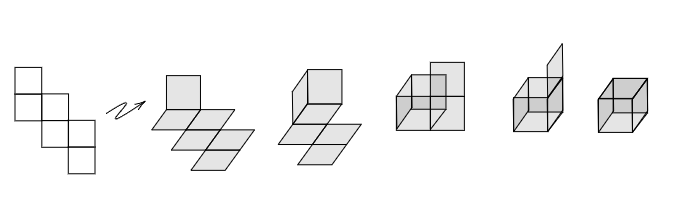
Imagine that you want to cover an endless floor with this cube net, so there are no gaps or overlaps, how would you lay them out? This is called covering or tiling the plane.

Cut a square into three parts and use these pieces to form a triangle whose angles are all acute (i.e: less than \(90^\circ\))

Jamie has a bag full of cards, where each card has a whole number written on it. How many cards must Jamie take from the bag to be certain that, among the cards chosen, there are at least two numbers whose average is also a whole number? Recall that to calculate the average of two numbers, we add them together and then divide by two.

Welcome back! The topic of this sheet is: dissections and gluings. This means that we will take shapes, break them apart, and put the pieces back together to form interesting objects. Sometimes, we will also “glue" objects together and see how they can be used to construct other shapes. Let’s see a few simple examples:

Long before meeting Snow White, the seven dwarves lived in seven different mines. There is an underground tunnel connecting any two mines. All tunnels were separate, so you could not start in one tunnel and somehow end up in another. Is it possible to walk through every tunnel exactly once without retracing your path?

The Pythagorean Theorem is one of the most important facts about geometry. It says that if we have a right-angled triangle (i.e: it has an angle of \(90^\circ\)), whose longest side measures \(C\), and its other two other sides measure \(A\) and \(B\):

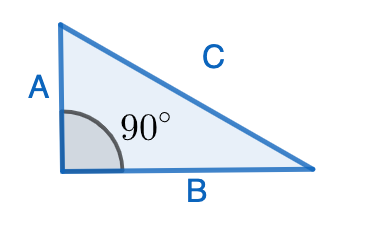
then \(A^2+B^2=C^2\). There are many proofs of this fact, and some involve dissections! Let’s have a look at the following two ways to dissect the same square:

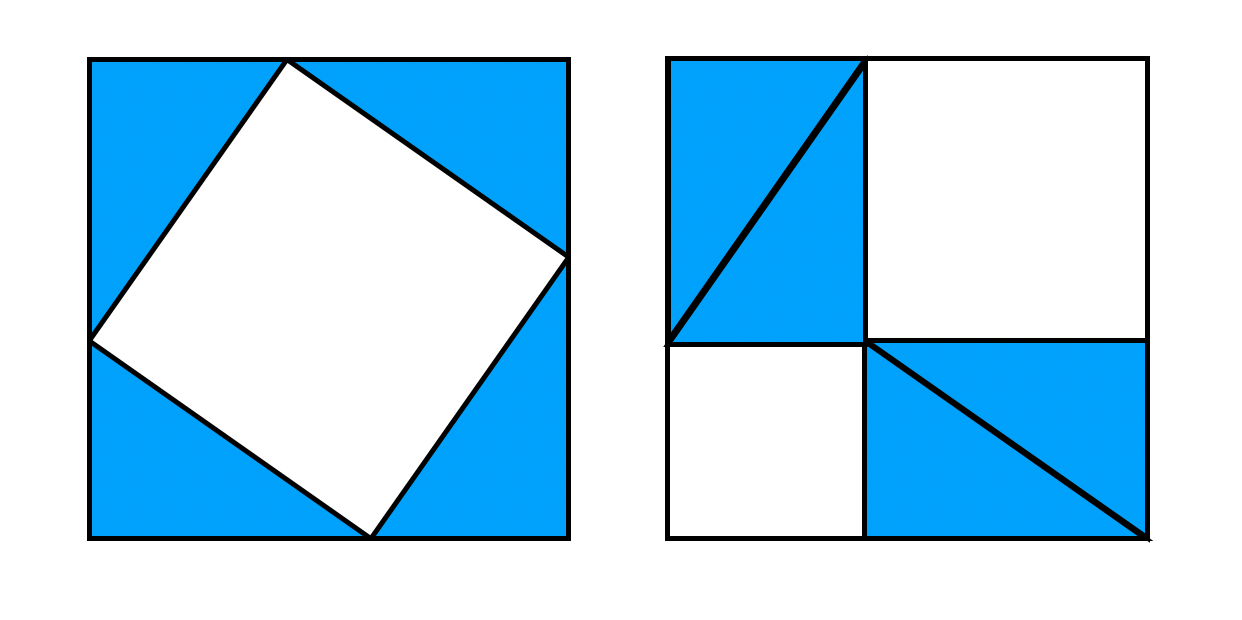
Can you explain how these dissections prove the Pythagorean Theorem?