Problems
Under a homothety transformation, a line \(l\) is sent to a line \(l'\) which is parallel to \(l\).
Show that a homothety is uniquely determined by where it sends any two distinct points.
Consider a homothety with center \(O\) and coefficient \(k\). Which lines are sent to themselves by this homothety? (Hint: the answer will depend on \(k\))
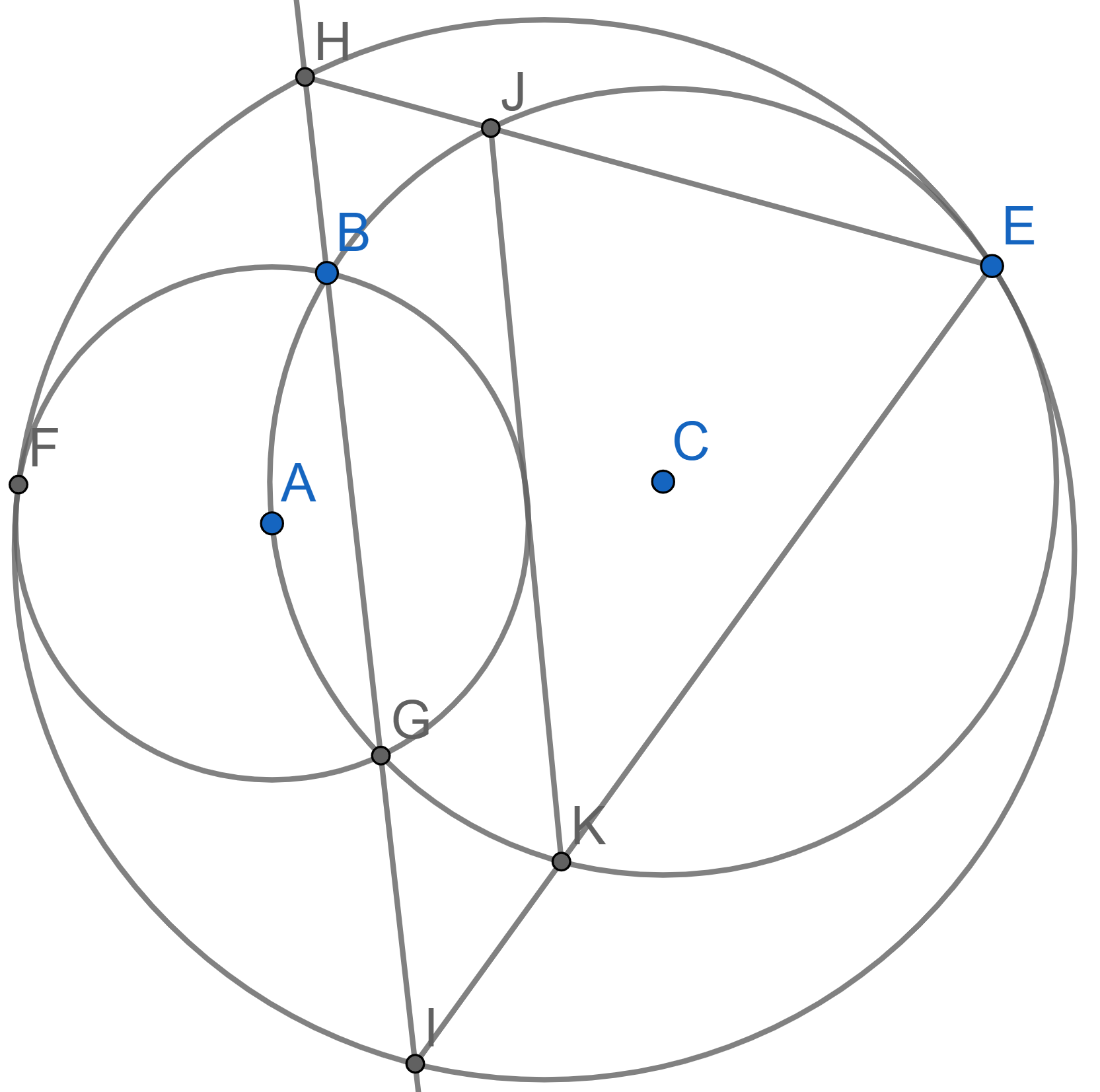
(IMO 1999) Two circles with centres \(A\) and \(C\) intersect at the points \(B\) and \(G\), moreover the circle with centre \(C\) goes through \(A\). A big circle is tangent to both given circles at the points \(E\) and \(F\) (see picture). The line \(BG\) intersects the big circle at the points \(H\) and \(I\). The segments \(EH\) and \(EI\) intersect with the circle with centre \(C\) at the points \(H\) and \(K\) respectively. Prove that the segment \(JK\) is tangent to the circle with center at \(A\).
On the first day Robinson Crusoe tied the goat with a single piece of rope by putting one peg into the ground. What shape did the goat graze?