Problems

On the Problemland Space Station, there are \(1000\) tonnes of air, of which \(99\%\) is oxygen. After an unfortunate asteroid impact, some of the air is vented into space. The hull is quickly repaired, and no further loss occurs.

Afterward, measurements reveal that oxygen now makes up only \(98\%\) of the remaining air, and that only oxygen was lost during the incident.

How many tonnes of oxygen remain on the space station?

In the following puzzle, different animals represent different digits, and your goal is to find which digit each animal represents.

Find all possible solutions.

What is the smallest positive whole number whose digits add up to \(2026\)?

The thirteen dwarves sat down around a bonfire in a circle, and their leader Thorin proposed a challenge to pass the time:

Each dwarf would choose an integer (it is not necessary that each dwarf chooses a different number) so that for every group of three neighboring dwarves, the sum of their numbers must be exactly \(13\).

Does Thorin’s challenge have a solution?

In the month of January of a certain year, there are exactly \(4\) Mondays and \(4\) Fridays. What day of the week is the \(20^{\text{th}}\) day of this month?

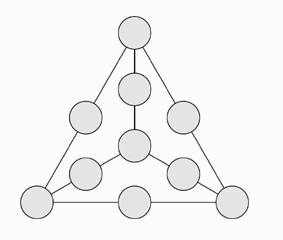
We would like to place the numbers \(1\) to \(10\) into the circles in the picture below, using each number exactly once, so that for every straight line of three circles, the numbers in those circles add up to the same total. Is this possible?

We have a \(17\) digit number, and we form a new number by reading the original number from right to left (if this produces a leading zero, we simply ignore this leading zero, giving a \(16\) digit number). We add this new number to the original number. Show that this resulting sum will have at least one even digit.

Which of the two following numbers is larger: \(31^{11}\) or \(17^{14}\)?

There are \(2026\) people at a big party. Some pairs of people are friends (nobody is friends with themselves, and friendship goes both ways). Starting one minute after midnight, the host begins sending people home in a strange way.

After 1 minute, anyone with no friends at the party leaves. After 2 minutes, anyone with exactly one friend currently in the party leaves. After 3 minutes, anyone with exactly two friends currently in the party leaves, and so on.

(Important: at each minute, everyone checks their number of friends at the same time, and then all the people who qualify leave together.)

Show that after \(2026\) minutes have passed, at least two people will have left the party.

Zippity the robot speaks a language of \(n\) words which can be written with \(0\)s and \(1\)s. In this language, no word appears as the first several digits of another word. For example: if “\(1001\)” is a word, then “\(100101\)” can’t be a word. Show that if \(\ell_1,\cdots, \ell_n\) are the lengths of each word (i.e: the number of digits), then \[\frac{1}{2^{\ell_1}}+\frac{1}{2^{\ell_2}}+\cdots + \frac{1}{2^{\ell_n}}\leq 1.\]