Problems

Two ants move along the same straight line and can only move back and forth along it. The first ant moves twice as fast as the second. Where could you place a breadcrumb so that the slower ant reaches it first?

Two ants, Muffy and Chip, start on opposite sides of a circle. Muffy moves twice as fast as Chip, and both can only move along the circle’s edge. Where could a breadcrumb be placed so that they both reach it at the same time?

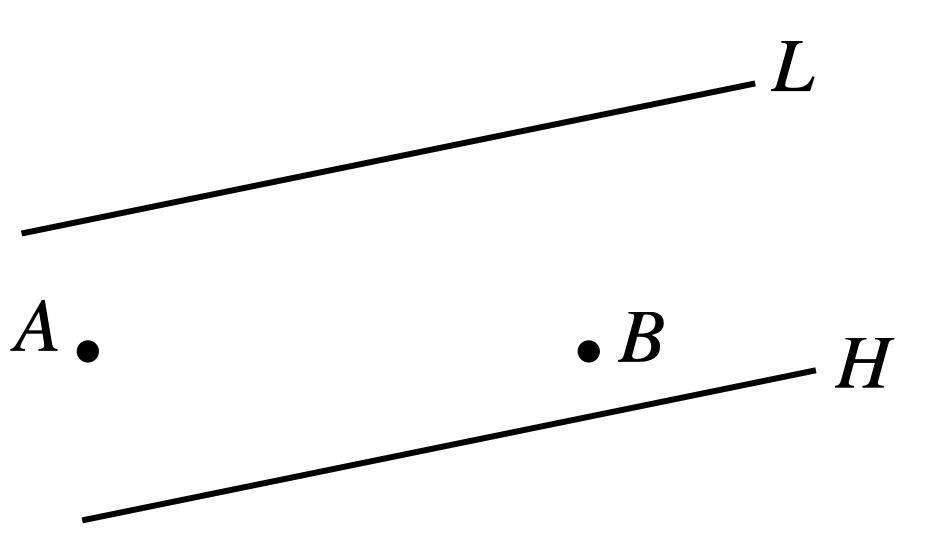
Two points, \(A\) and \(B\), lie between two lines \(L\) and \(H\). Draw the shortest path from \(A\) to \(B\) that touches \(L\), then \(H\), and finally reaches \(B\).

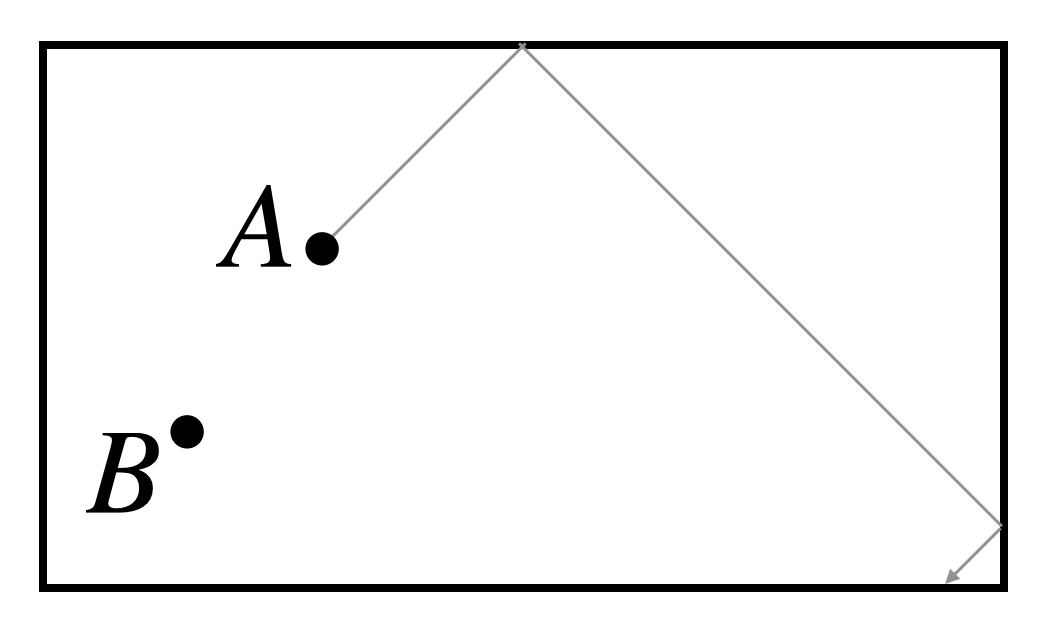
Ignat is playing pool and places a ball at point \(A\), as shown below. Can he bounce ball \(A\) off a ball placed at position \(B\), if the ball can only bounce off the top and right edges of the pool table?

When a ball bounces off the edge, it does so just like light reflecting in a mirror: the angle at which it hits the edge is the same as the angle at which it bounces away.

A ball \(A\) is placed on the pool table as shown below. The walls are labeled as follows: wall \(1\) is the top wall, wall \(2\) is the right wall, wall \(3\) is the bottom wall, and wall \(4\) is the left wall.

If we hit the ball so that it bounces off the walls labeled \(1\), \(2\), \(3\), and \(4\) —in that order—and then stops rolling just before hitting the next wall, what region of the pool table can the ball reach? If the ball hits a corner, it also stops.

A point \(A\) is placed on the bottom edge of a cylinder, along the rim of the lower circle. Another point \(B\) is placed on the top circle, but opposite to opposite to \(A\), so that \(A\) and \(B\) are as far away as possible from each other.

Find the shortest path along the curved surface of the cylinder that goes from \(A\) to \(B\).