Problems
Is it possible to arrange \(10\) numbers in a row such that:
The sum of any \(4\) consecutive numbers is positive.
The sum of any \(5\) consecutive numbers is positive.
The sum of any \(7\) consecutive numbers is negative?
In how many different ways can you place \(12\) chips in the squares of a \(4\times 4\) board so that
there is at most one chip in each square, and
every row and every column contains exactly three chips?
On a TV screen the number \(1\) appears. Every minute that passes by, the number that is currently on the screen increases by the sum of its digits. For example: if at some point the number \(12\) appears on the screen, the next number will be \(12+(1+2)=15.\) Will the number \(123456\) ever appear on the screen?
Seven vertices of a cube are labelled with the number \(0\), and the remaining vertex is labelled with \(1\). You are allowed to repeat the following move: choose an edge of the cube and increase by \(1\) the numbers at both ends of that edge.
Is it possible to reach eight numbers that are all divisible by three?
Each number on the number line (not only whole numbers!) is painted black \((B)\) or white \((W)\). Is it always possible, regardless of how the number line is painted, to find a line segment such that both its endpoints and its middle point are painted with the same colour?
A book club with 37 members is reading the following books: “Brave New World", “Dracula" and “Flatland". Each member chose one of the books, though some people chose more than one book. We know that:
23 people chose “Brave New World";
18 people chose “Dracula";
26 people chose “Flatland";
7 people chose all three books.
How many people chose at least two books?
Jan wants to paint a map with \(95\) countries on it, where only one colour can be used for each country. He has \(33\) different colours to paint with and he must use each of yellow, blue, green, purple and red at least once. How many ways of painting the map are there?
We are going to play the following game: look at the grid below, where each cell is painted black or white

choose any two cells that are next to each other and switch both of their colours. By switch, we mean: if a cell is black, change it to white, and if it is white, change it to black. Is it possible to turn the entire grid black?
A convex polygon \(A_1A_2...A_n\) has the following property: if we parallel push all the lines containing the sides of the polygon for a distance \(1\) outside, we will obtain another polygon, similar to the original one with the corresponding parallel sides of the same ratio. Prove that one can inscribe a circle into the original polygon \(A_1A_2...A_n\).
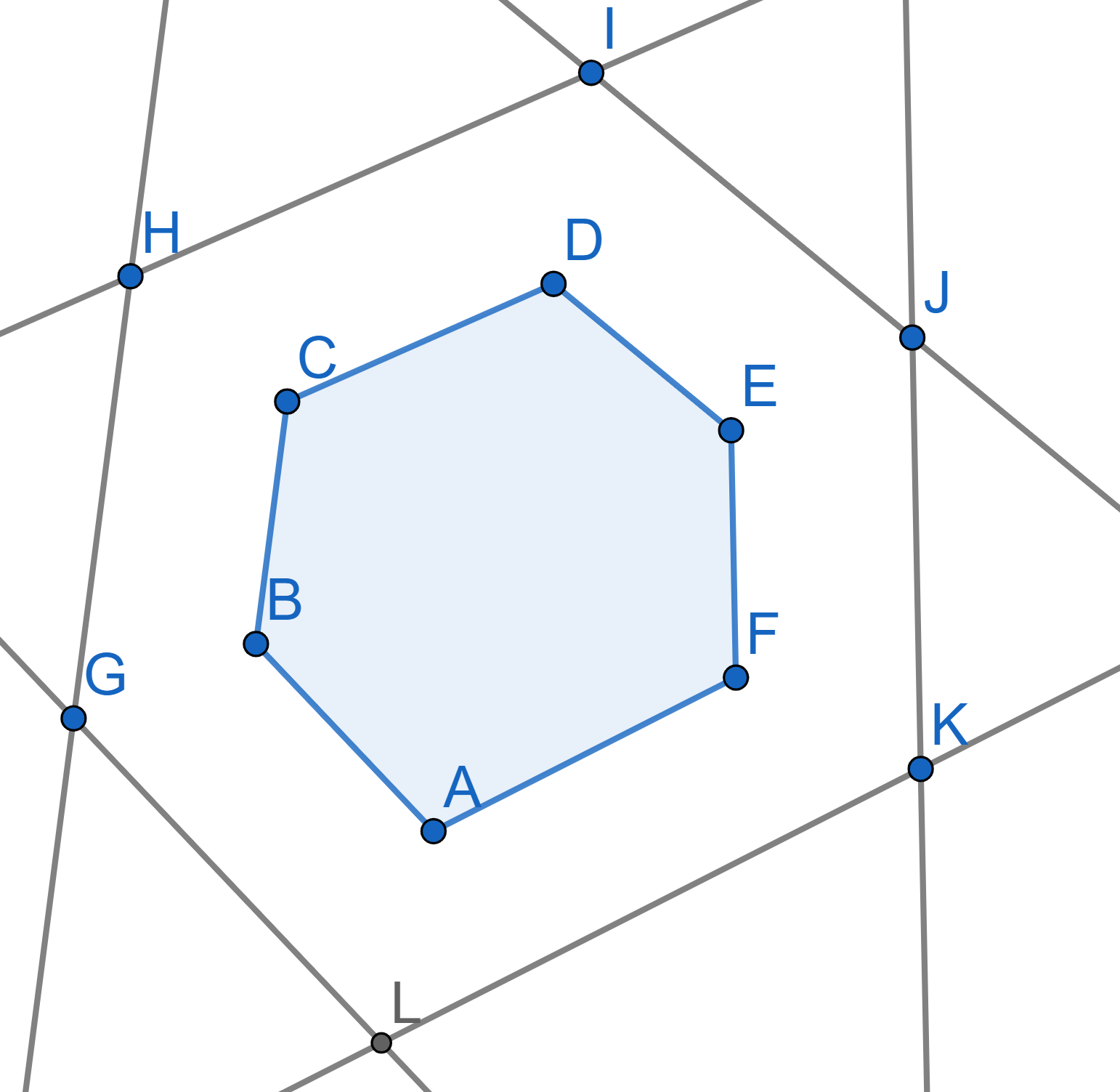
For a triangle \(ABC\) denote by \(R\) the radius of the circle superscribed around \(ABC\), by \(r\) the radius of circle inscribed into \(ABC\). Prove that \(R\geq 2r\) and equality holds if and only if the triangle \(ABC\) is regular. For this problem, you may want to search about the “Euler Circle” online.