Problems
Sometimes geometric problems are solved using a variety of plane transformations. One of such transformations is called Homothety. It requires the following data:
The center of homothety: a point on the plane, we will usually denote it as \(O\).
The koefficient of homothety: a real number, we will denote it as \(k\).
The plane transformation is described in the following way: every point \(X\) on the plane is sent to a point \(X'\) with the following properties: The points \(O, X, X'\) lie on one line, in that exact order for a coefficient \(k \geq 1\).
The distance \(OX' = kOX\).
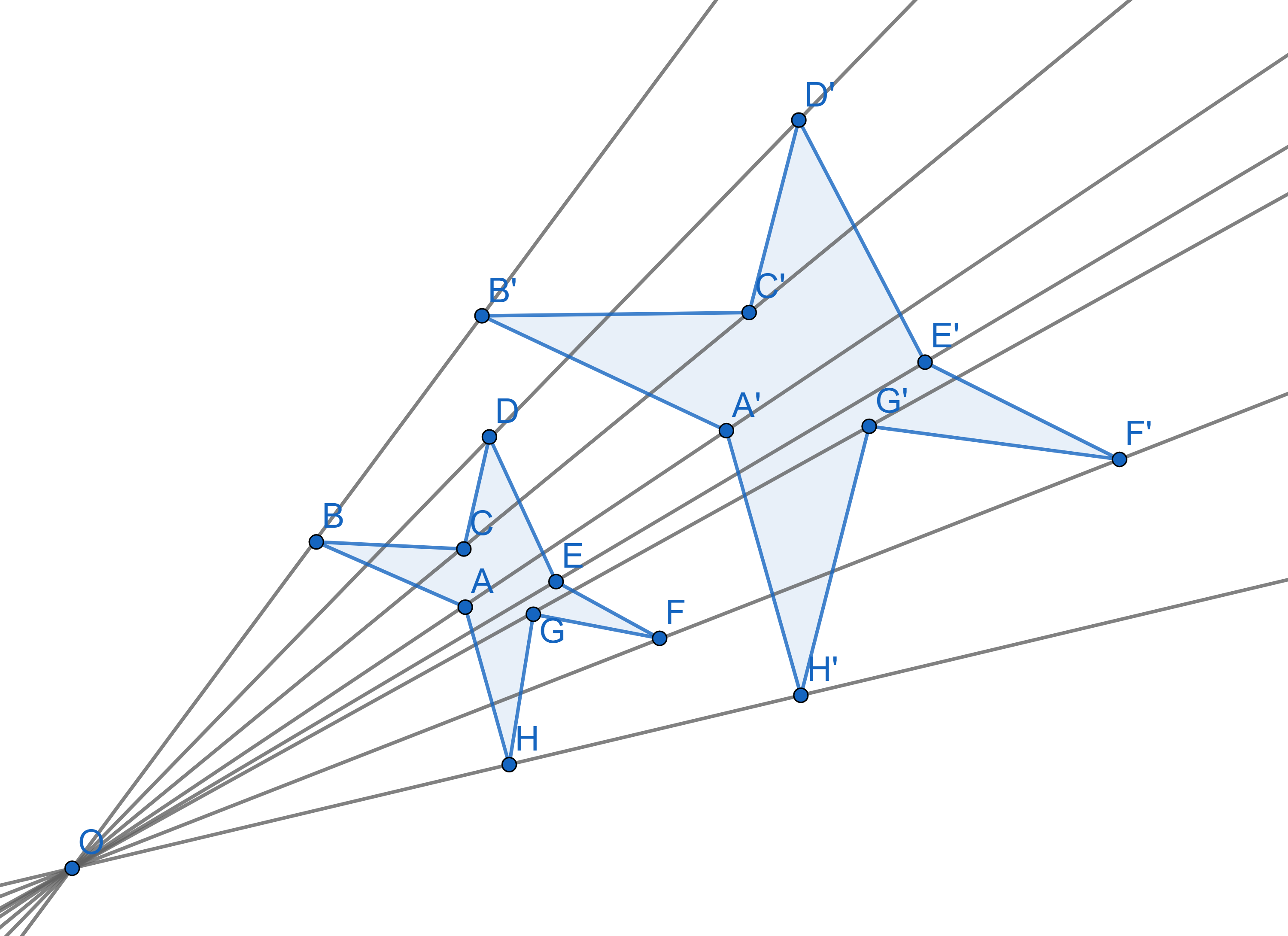
Prove that under the homothety transformation, a circle is transferred into a circle. Consider all possible cases of \(k\): \(k<0, 0<k \leq 1, 1\leq k\).
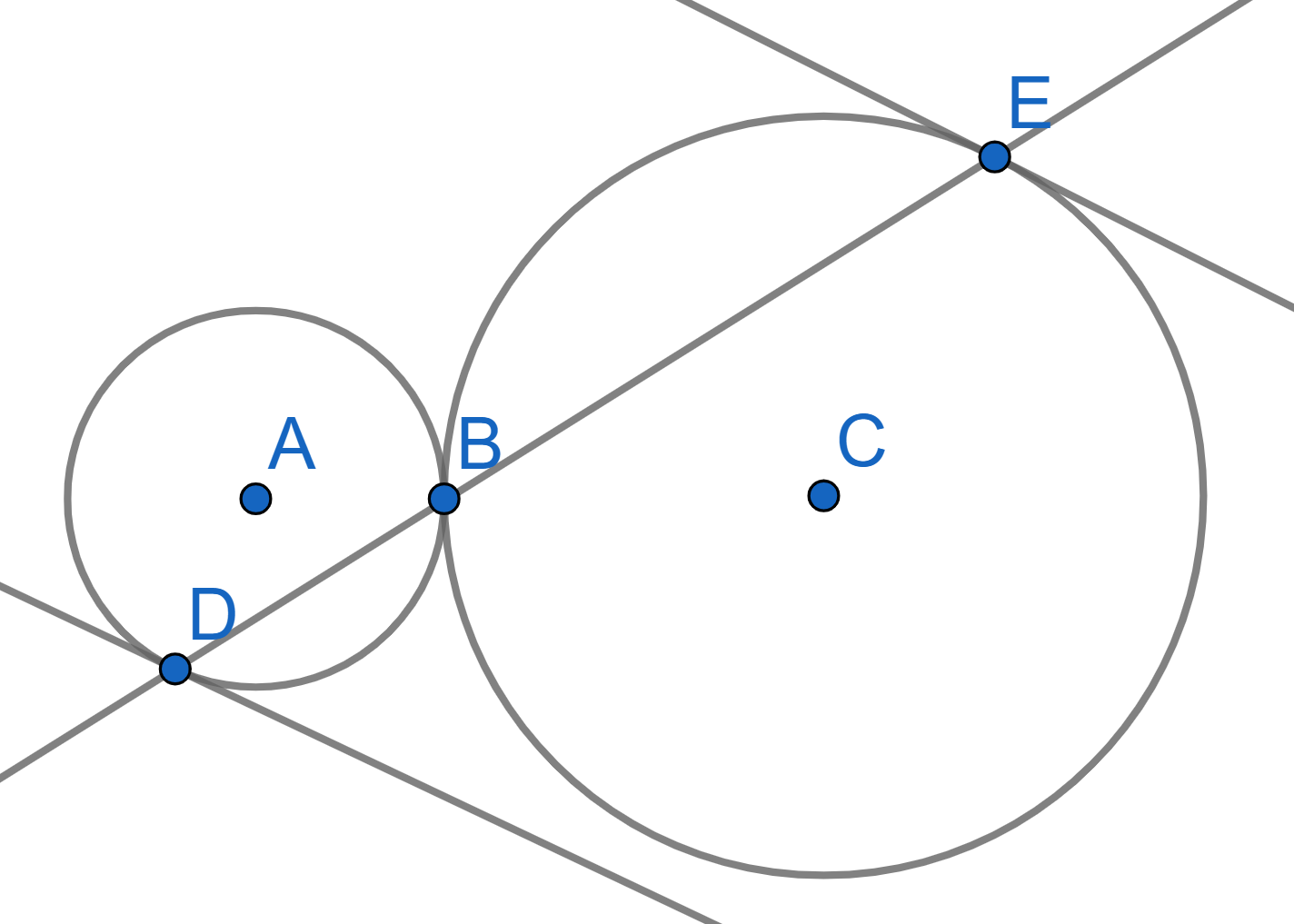
Two circles with centres \(A\) and \(C\) are tangent at the point \(B\). The segment \(DE\) passes through the point \(B\). Prove that the tangent lines passing through the points \(D\) and \(E\) are parallel.