Problems

In the trapezium \(ABCD\) the point \(E\) is the point of intersection of the sides \(AB\) and \(CD\), the point \(G\) is the point of intersection of diagonals, the points \(F,H\) are the midpoints of the sides \(BC\) and \(AD\) respectively.

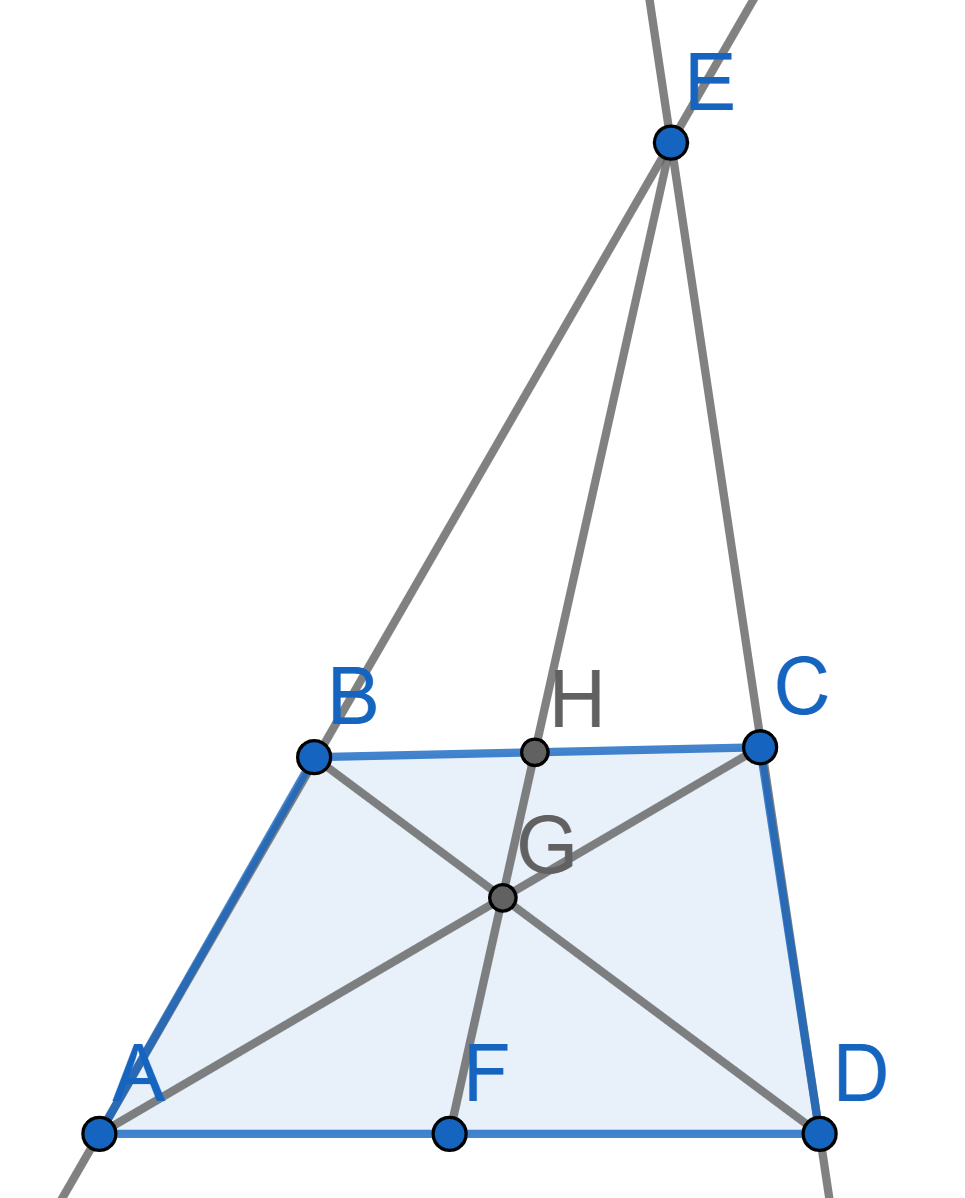
Prove that the points \(E,F,G,H\) lie on one line.

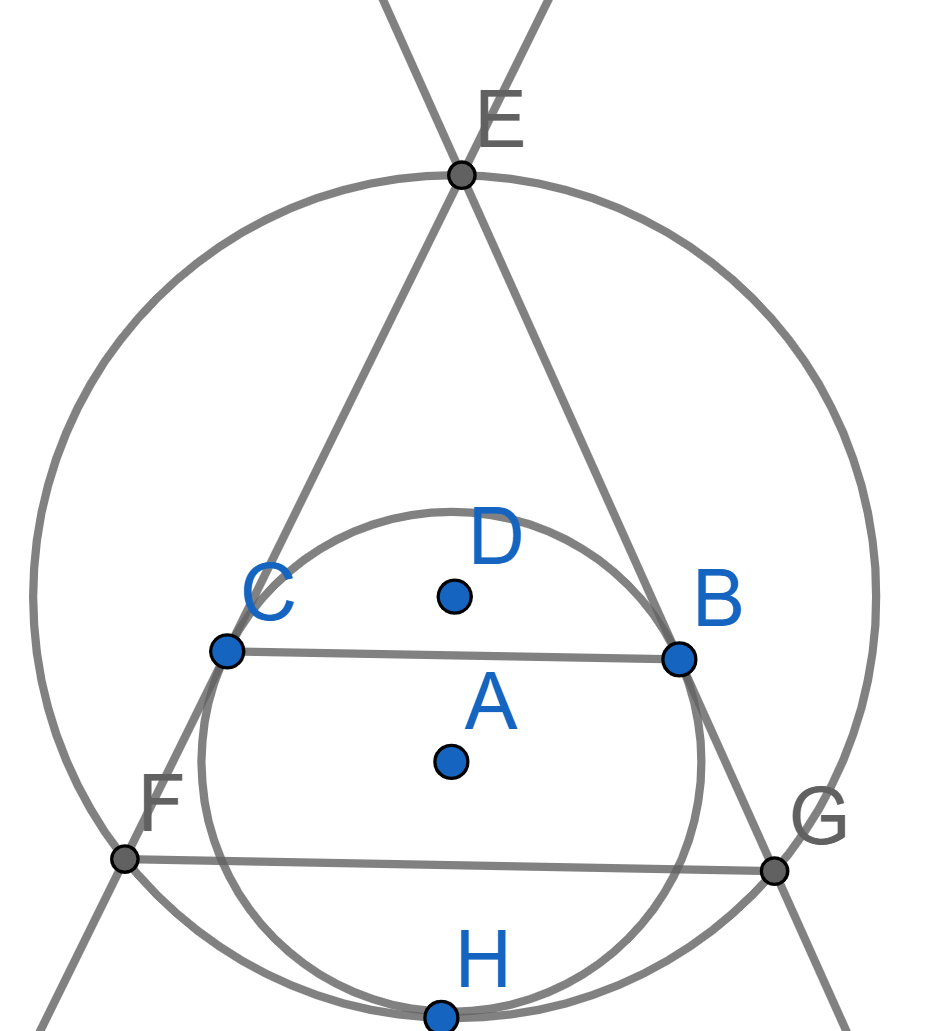
The triangle \(EFG\) is equilateral and \(EF=EG\). A circle with center \(A\) is tangent to the sides \(EF\) and \(EG\) at the points \(C\) and \(B\) respectively. It is also tangent to the circle circumscribed around the triangle \(EFG\) at the point \(H\). Prove that the midpoint of the segment \(BC\) is the center of the circle inscribed into he triangle \(EFG\).