Problems

Jan wants to paint a map with \(95\) countries on it, where only one colour can be used for each country. He has \(33\) different colours to paint with and he must use each of yellow, blue, green, purple and red at least once. How many ways of painting the map are there?

We are going to play the following game: look at the grid below, where each cell is painted black or white

choose any two cells that are next to each other and switch both of their colours. By switch, we mean: if a cell is black, change it to white, and if it is white, change it to black. Is it possible to turn the entire grid black?

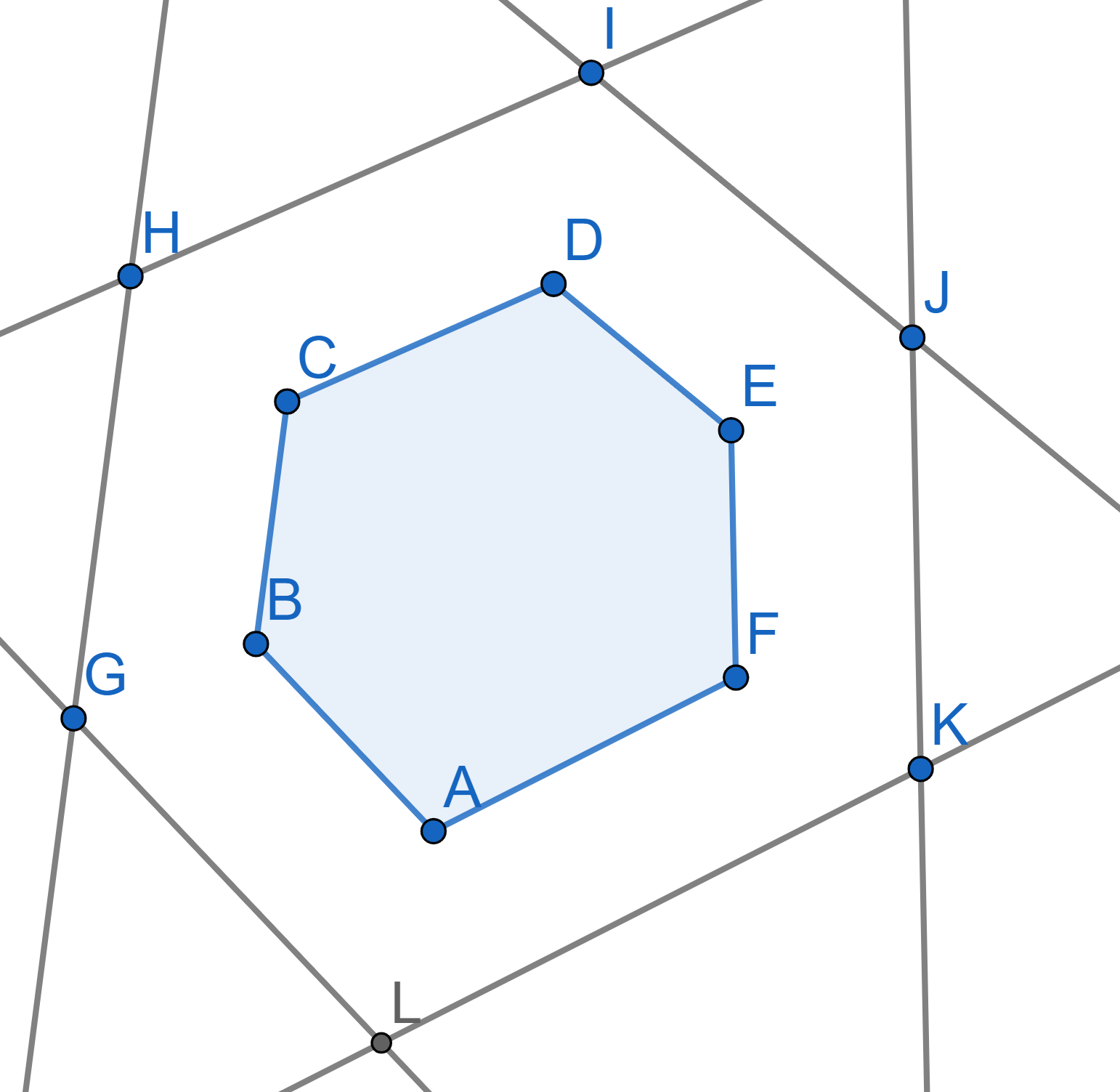
A convex polygon \(A_1A_2...A_n\) has the following property: if we parallel push all the lines containing the sides of the polygon for a distance \(1\) outside, we will obtain another polygon, similar to the original one with the corresponding parallel sides of the same ratio. Prove that one can inscribe a circle into the original polygon \(A_1A_2...A_n\).

For a triangle \(ABC\) denote by \(R\) the radius of the circle superscribed around \(ABC\), by \(r\) the radius of circle inscribed into \(ABC\). Prove that \(R\geq 2r\) and equality holds if and only if the triangle \(ABC\) is regular.