Problems
A stoneboard was found on the territory of the ancient Greek Academia as a result of archaeological excavations.
The archeologists decided that this stoneboard belonged to a mathematician who lived in the 7th century BC. The list of unsolved problems was written on the stoneboard. The archaeologists became thrilled to solve the problems but got stuck on the fifth. They were looking for a 10-digit number. The number should consist of only different digits. Moreover, if you cross any 6 digits, the remaining number should be composite. Can you help the archeologists to figure out the answer?
Find three different natural numbers, larger than \(100\) such that each of them is divisible by the difference of the other two numbers? The values of differences also have to be different from each other.
Divide 15 walnuts into four groups, each group consisting of a different whole number of nuts.
In the following example with fractions replace “stars” with different natural numbers in order to obtain an identity: \[\frac{1}{*}+\frac{1}{*}=\frac{1}{*}+\frac{1}{*}.\]
Looking back at Example 12.1 what if we additionally require all differences to be less than the smallest of the three numbers?
(a) Divide 55 walnuts into four groups consisting of different number of nuts.
(b) Divide 999 walnuts into four groups consisting of different number of nuts.
Replace "stars" with different natural numbers in order to obtain an
identity:
\[\frac{1}{*}+\frac{1}{*}+\frac{1}{*}=\frac{1}{*}+\frac{1}{*}+\frac{1}{*};\]
George knows a representation of number “8” as the sum of its divisors in which only divisor “1” appears twice: \[8=4+2+1+1.\] His brother showed George that such representation exists for number “16” as well: \[16=8+4+2+1+1.\] He apologies for forgetting an example considering number “32” but he is sure once he saw such representation for this number.
(a) Help George to work out a suitable representation for number “32”;
(b) Can you think of a number which has such representation consisting of 7 terms?
(c) Of 11 terms?
(d) Can you find a number which can be represented as a sum of its divisors which are all different (pay attention that we don’t allow repeating digit “1” twice!)?
(e) What if we require this representation to consist of 11 terms?
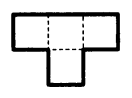
Two figures are said to be similar if all their corresponding sides
are congruent and corresponding angles are equal. By using several
copies of the figure below construct a bigger figure that is
similar.
Divide a square into several triangles in such a way that every triangle shares a boundary with exactly three other triangles.