Problems
In the context of Example 14.2 what is the answer if we have five numbers instead of four? (i.e., can we get four distinct prime numbers then?)
Now George is sure he found two numbers with the quotient equal to their sum. And on top of that their product is still equal to the same value. Can it be true?
A maths teacher draws a number of circles on a piece of paper. When she shows this piece of paper to the young mathematician, he claims he can see only five circles. The maths teacher agrees. But when she shows the same piece of paper to another young mathematician, he says that there are exactly eight circles. The teacher confirms that this answer is also correct. How is that possible and how many circles did she originally draw on that piece of paper?
A group of three smugglers is offered to smuggle a chest full of treasures across the dangerous river. The boat they possess is old and frail. It can carry three smugglers without the chest, or it can carry the chest and only two smugglers. The price for this job is extremely high, and the gang is more than interested in completing the job. Think of a strategy the smugglers should follow to successfully transit the chest and themselves to the other shore.
It is easy to construct one equilateral triangle from three identical matches. Can we make four equilateral triangles by adding just three more matches identical to the original ones?
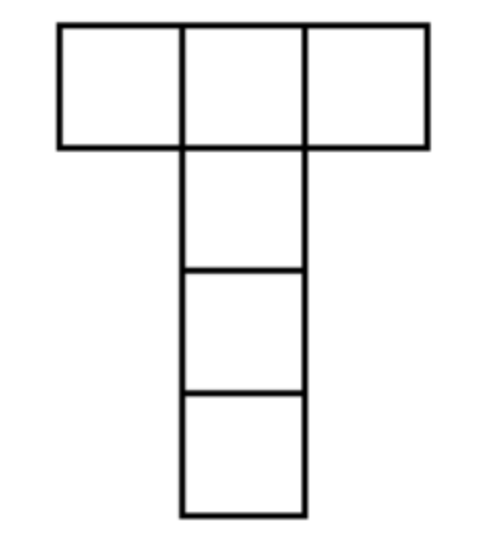
What is the smallest whole number \(n\) such that four identical T-shaped pieces (as shown below) can be placed inside an \(n\times n\) square grid without overlapping?
After having lots of practice with cutting different hexagons with a single cut Jennifer thinks she found a special one. She found a hexagon which cannot be cut into two quadrilaterals. Provide an example of such a hexagon.
My mum once told me the following story: she was walking home late at night after sitting in the pub with her friends. She was then surrounded by a group of unfriendly looking people. They demanded: “money or your life?!” She was forced to give them her purse. She valued her life more, since she was pregnant with me at that time. According to her story she gave them two purses and two coins. Moreover, she claimed that one purse contained twice as many coins as the other purse. Immediately, I thought that the mum must have made a mistake or could not recall the details because of the shock and the amount of time that passed after that moment. But then I figured out how this could be possible. Can you?
A new airline "Capitals Direct" has direct flights operating on the following routes (in both directions): Paris - London, Paris - Lisbon, Rome - London, Rome - Madrid, Berlin - Helsinki, Berlin - Amsterdam, Amsterdam - Prague. These are the only flights that the company offers. I would like to travel from Paris to Amsterdam. I cannot buy a direct ticket for sure, but can "Capitals Direct" offer me a connecting flight?
Can one arrange numbers from \(1\) to \(9\) in a row so that each pair of consecutive numbers forms a two-digit multiple of \(7\) or a multiple of \(13\)?