Problems
The height \(SO\) of a regular quadrilateral pyramid \(SABCD\) forms an angle \(\alpha\) with a side edge and the volume of this pyramid is equal to \(V\). The vertex of the second regular quadrangular pyramid is at the point \(S\), the centre of the base is at the point \(C\), and one of the vertices of the base lies on the line \(SO\). Find the volume of the common part of these pyramids.
100 queens, that cannot capture each other, are placed on a \(100 \times 100\) chessboard. Prove that at least one queen is in each \(50 \times 50\) corner square.
In 25 boxes there are spheres of different colours. It is known that for any \(k\) where \(1 \leq k \leq 25\) in any \(k\) of the boxes there are spheres of exactly \(k+1\) different colours. Prove that a sphere of one particular colour lies in every single box.
The sequence \((a_n)\) is given by the conditions \(a_1 = 1000000\), \(a_{n + 1} = n \lfloor a_n/n\rfloor + n\). Prove that an infinite subsequence can be found within it, which is an arithmetic progression.
Given a square trinomial \(f (x) = x^2 + ax + b\). It is known that for any real \(x\) there exists a real number \(y\) such that \(f (y) = f (x) + y\). Find the greatest possible value of \(a\).
In the infinite sequence \((x_n)\), the first term \(x_1\) is a rational number greater than 1, and \(x_{n + 1} = x_n + \frac{1}{\lfloor x_n\rfloor }\) for all positive integers \(n\).
Prove that there is an integer in this sequence.
Note that in this problem, square brackets represent integers and curly brackets represent non-integer values or 0.
On the plane coordinate axes with the same but not stated scale and the graph of the function \(y = \sin x\), \(x\) \((0; \alpha)\) are given.
How can you construct a tangent to this graph at a given point using a compass and a ruler if: a) \(\alpha \in (\pi /2; \pi)\); b) \(\alpha \in (0; \pi /2)\)?
A game of ’Battleships’ has a fleet consisting of one \(1\times 4\) square, two \(1\times 3\) squares, three \(1\times 2\) squares, and four \(1\times 1\) squares. It is easy to
distribute the fleet of ships on a \(10\times
10\) board, see the example below. What is the smallest square
board on which this fleet can be placed? Note that by the rules of the
game, no two ships can be placed on horizontally, vertically, or
diagonally adjacent squares.

The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.
Prove that if the expression
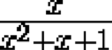
takes a rational value, then the expression
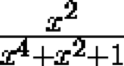
also takes on a rational value.